Wolfram Demonstrations Project

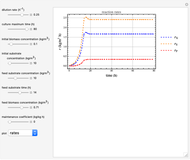
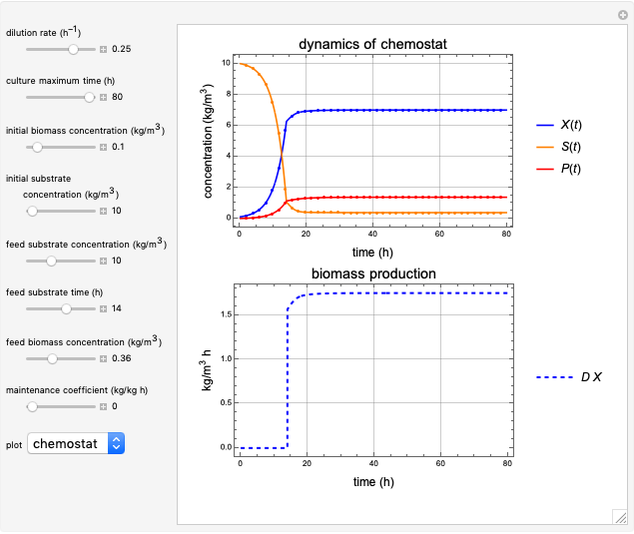
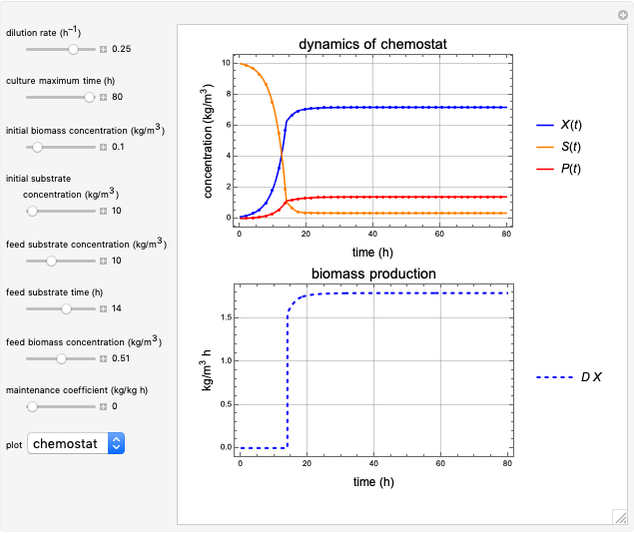
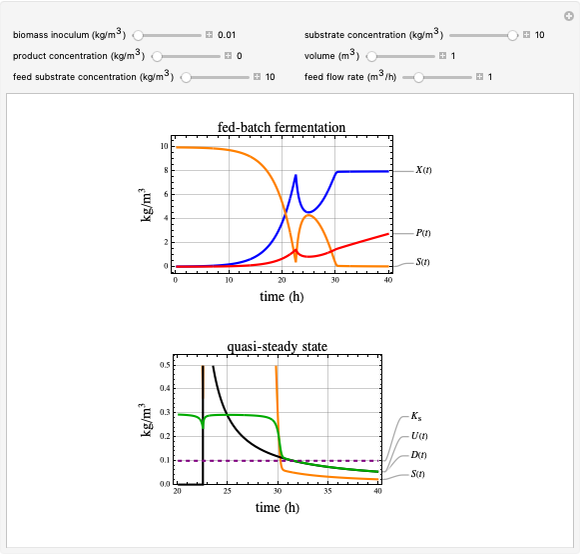
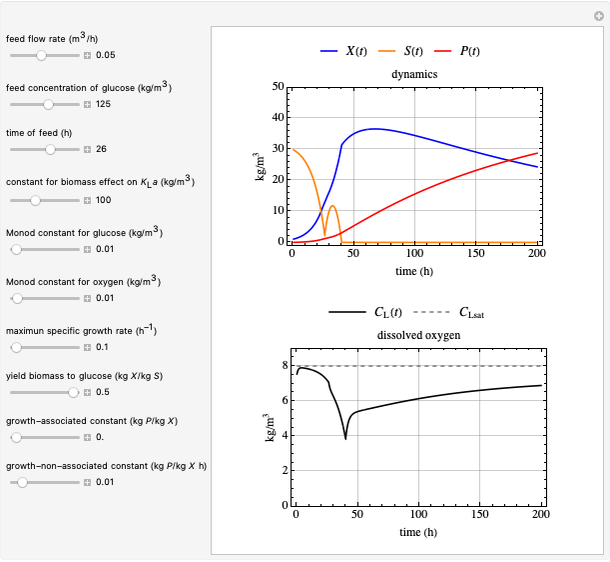
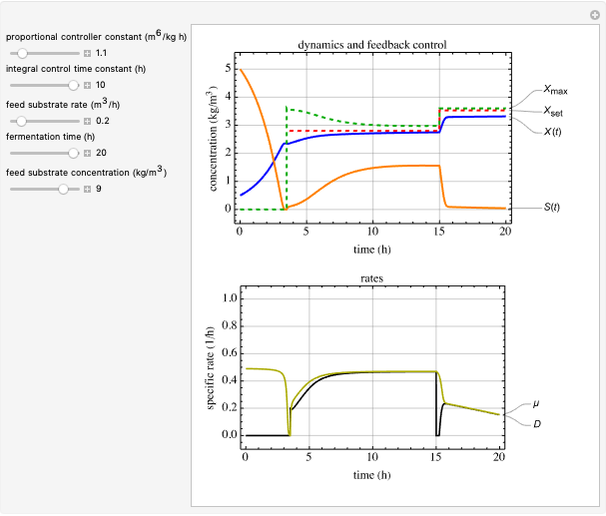
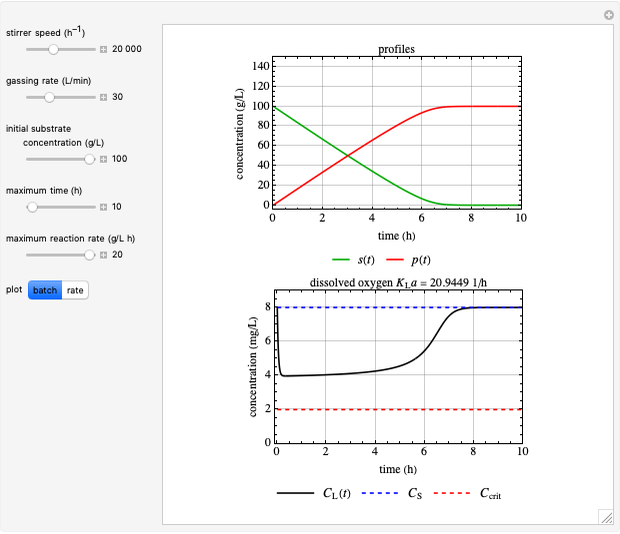
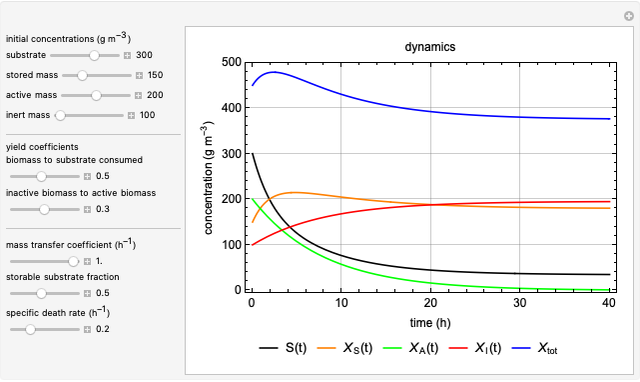
This Demonstration shows the operation of a chemostat. Starting up as a batch reactor, the concentrations change with time. After this short transient period, the bioreactor settles into a steady state.

The behavior of a chemostat, also called a continuous reactor, can be characterized by the concentration profiles of the reactants and products.

In this Demonstration,

is time,

is the concentration of a reactant consumed (also called the substrate),

is the biomass (or cell) concentration,

is the concentration of a product and

is the dilution rate. The concentration in a perfectly mixed tank is uniform throughout the vessel and is therefore identical to the concentration of the effluent stream.

Contributed by: R. Ricardo Sánchez

Slider Zoom
Gamepad Controls
Automatic Animation

The characteristics of continuous operation are as follows:

Snapshot 1: steady state; after an initial startup period, there is no variation of concentrations with time

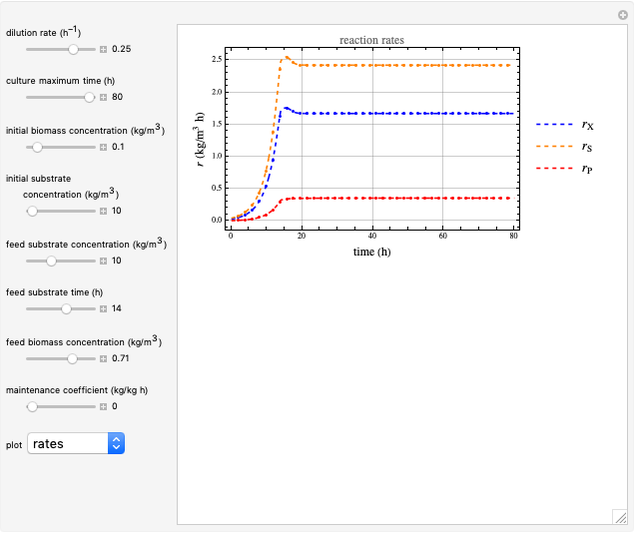
Snapshot 2: constant reaction rates, where

is the biomass reaction rate,

is the reaction rate of the consumed reactant and

is the product reaction rate

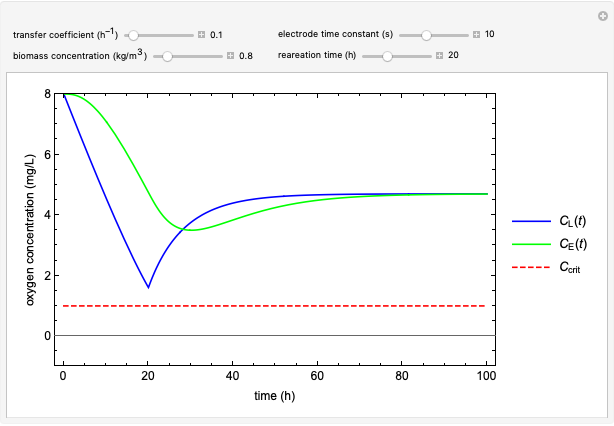
Snapshot 3: Washout of the organisms (cells) will occur when the dilution rate

is greater than the specific growth rate

. This corresponds to the complete removal of cells by flow out of the tank. In many references, including [1], the variables

and productivity

are plotted versus the dilution rate

, which characterizes the steady state in a chemostat. See Related Links.

Some suggestions for the user:

Increase

interactively to note effect on washout.

Change the feed substrate concentration

to alter the steady state.

Investigate the influence of maintenance requirements on the steady-state biomass concentration.

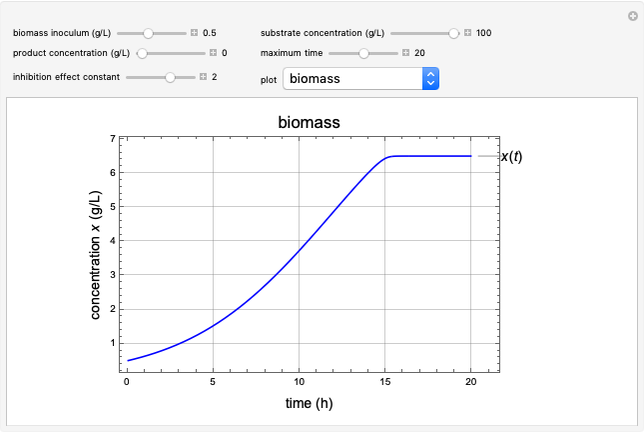
Operate initially as a batch reactor with

, and switch to chemostat operation with

is the maximum specific growth rate, and in this case was set up to

Calculate

, the biomass-substrate yield, making use of the yield graph.

Reference

[1] I. J. Dunn, E. Heinzle, J. Ingham and J. E. Přenosil, Biological Reaction Engineering: Dynamic Modelling Fundamentals with Simulation Examples, Second Edition, Weinheim, Germany: Wiley-VCH, 2003.