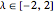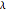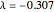Symmetrizing Positive Random Variables

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
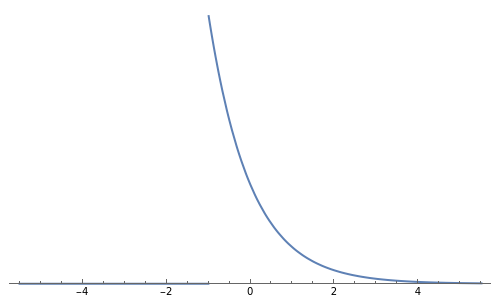
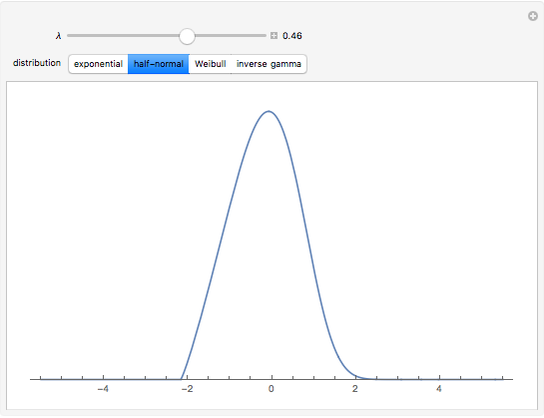
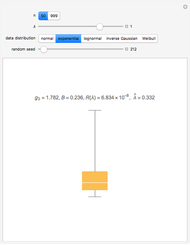
Transformations to symmetry are frequently used in statistics to improve the accuracy of statistical models that assume the normal distribution or at least symmetrically distributed errors. Typically the transformation is chosen after the data has been observed but it is of theoretical interest to see what is the best symmetrizing transformation for various possible distributions.
[more]
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
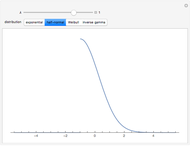
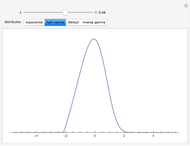
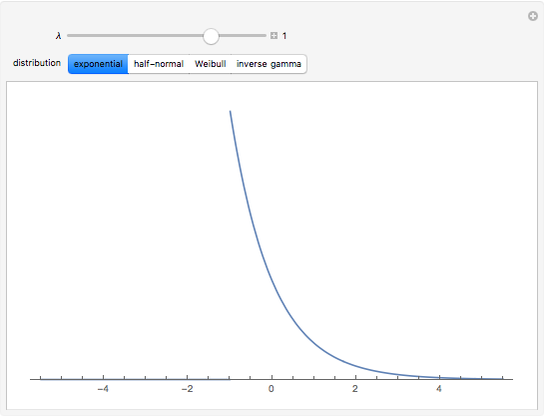
Snapshots
Details
Let 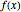 be the probability density function of
be the probability density function of 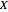 with support on
with support on 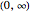 and let
and let 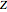 be defined by
be defined by
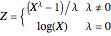 .
.
Then for 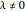 , the probability density function for
, the probability density function for 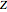 may be written
may be written
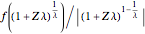
with support on 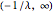 for
for 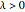 and on
and on  for
for 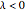 . For
. For  , the probability density function is
, the probability density function is 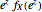 with support on
with support on  . The derivation of this result is within the scope of a first course in mathematical statistics.
. The derivation of this result is within the scope of a first course in mathematical statistics.
Power transformations, 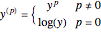 ,
,
are frequently used to improve the statistical assumption of normal or symmetrically distributed response variables in many situations in applied statistics. The family of Box–Cox transformations [1] given by
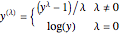
is often preferred for mathematical analysis and visualization since they are monotonic (or order preserving) and continuous at  . But for interpretability, it is sometimes more convenient to use a simple member of the power transformation family, for example, square root or log.
. But for interpretability, it is sometimes more convenient to use a simple member of the power transformation family, for example, square root or log.
It is interesting that for the four distributions considered, the variance is proportional to or approximately proportional to the square of the mean and hence the logarithmic transformation is the variance-stabilizing transformation [2]. This Demonstration shows that the best symmetrizing transformation is not so simple and, further, lets you compare these transformations graphically.
[1] G. E. P. Box and D. R. Cox, "An Analysis of Transformations," Journal of the Royal Statistical Society B, 26(2), 1964 pp. 211–252.
[2] M. S. Bartlett, "The Use of Transformations," Biometrics, 3(1), 1947 pp. 37–52.
Permanent Citation