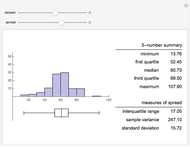
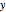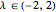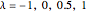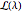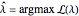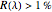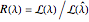Choosing a Data Transformation with the Box-Whisker Plot

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration shows the effect of a power data transformation,
[more]
Contributed by: Ian McLeod (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
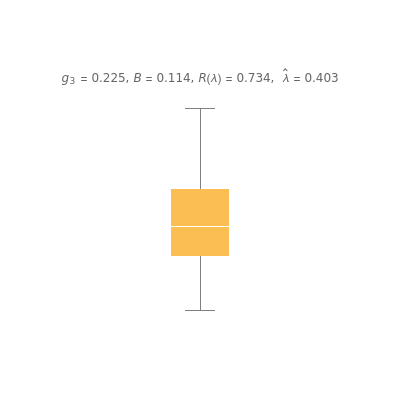
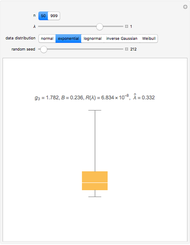
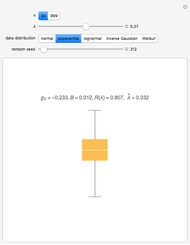
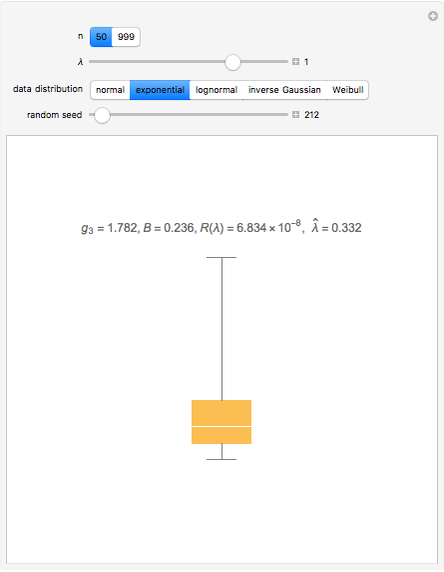
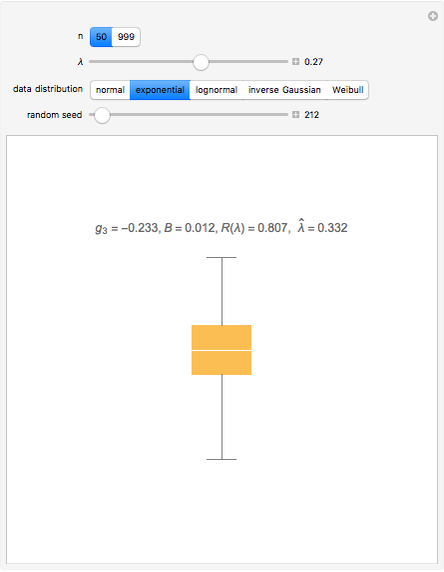
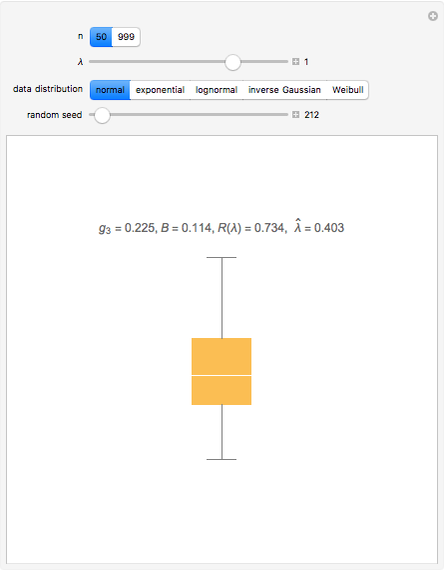
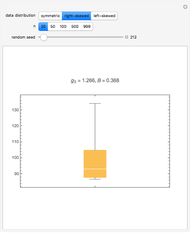
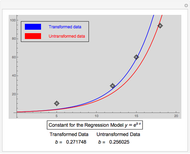
Data transformations such as square-root and logs are often used in statistics to improve the model assumptions. See [1] for examples, with actual data, of the use of box-and-whisker plots to choose a transformation.
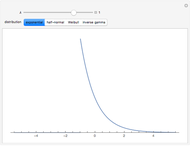
Using Mathematica's built-in functions Manipulate and BoxWhisker with the family of power transformations provides a simple and effective method for choosing a suitable transformation with real data. For comparison and for pedagogical purposes, we have included skewness and maximum likelihood methods for choosing 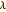 .
.
[2] discusses the use of maximum likelihood estimation for 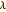 in the family of power transformations,
in the family of power transformations,
 .
.
[3] discusses choosing a power transformation by minimizing absolute skewness. The robust skewness statistic computed using QuartileSkewness is sometimes called Bowley skewness (Wolfram MathWorld).
The use of the relative likelihood function for statistical inference is discussed in the books [4] and [5].
References:
[1] W. S. Cleveland, Visualizing Data, Summit, NJ: Hobart Press, 1993.
[2] G. E. P. Box and D. R. Cox, "An Analysis of Transformations," Journal of the Royal Statistical Society B, 26(2), 1964 pp. 211–252.
[3] D. V. Hinkley, "On Power Transformations to Symmetry,” Biometrika, 62, 1975 pp. 101–111.
[4] A. Azzalini, Statistical Inference, Boca Raton, FL: Chapman & Hall/CRC, 1996.
[5] D. A. Sprott, Statistical Inference in Science, New York: Springer, 2000.
Permanent Citation