Vapor-Liquid Equilibrium Data Using Arc Length Continuation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
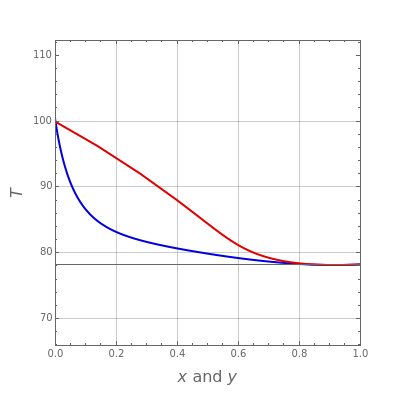
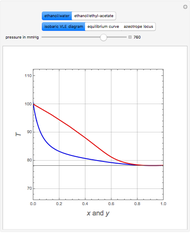
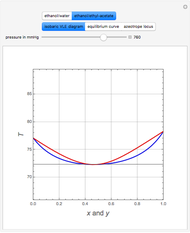
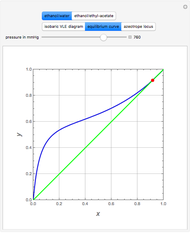
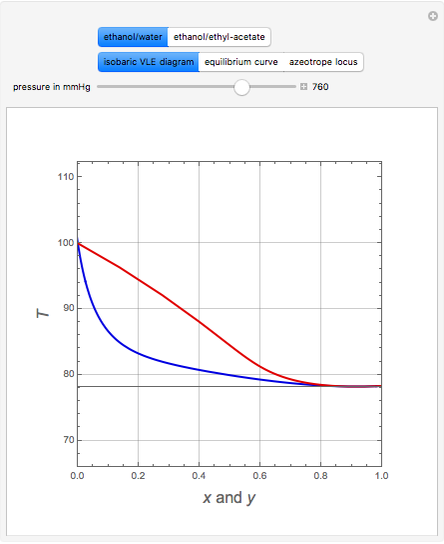
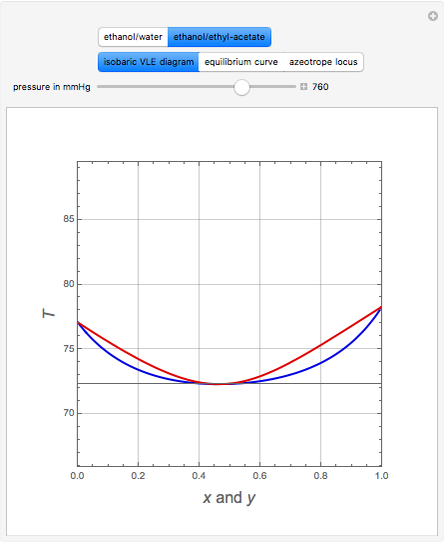
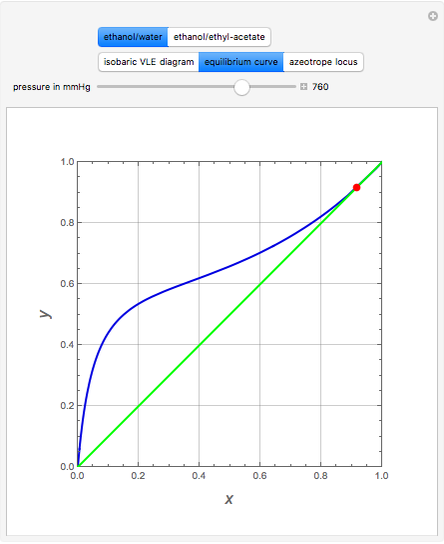
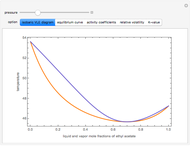
Consider two binary mixtures: (1) ethanol and water and (2) ethanol and ethyl acetate. This Demonstration computes the isobaric vapor-liquid diagram as well as the equilibrium curve at user-set values of the total pressure  (expressed in
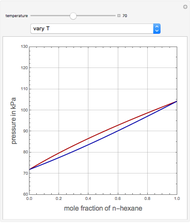
(expressed in  ). The modified Raoult's law is used along with the van Laar model and Antoine equation. Both systems present a positive pressure-sensitive azeotrope. When present, this azeotrope is indicated on the equilibrium curve by a red dot. The loci of the azeotrope versus pressure
). The modified Raoult's law is used along with the van Laar model and Antoine equation. Both systems present a positive pressure-sensitive azeotrope. When present, this azeotrope is indicated on the equilibrium curve by a red dot. The loci of the azeotrope versus pressure  is given in a separate plot. In both cases, the azeotrope disappears at a low enough total pressure. One particular feature of the present calculation is that it uses the arc length continuation method (see the Details section) to find the bubble/dew point temperatures versus liquid/vapor phase compositions. This takes advantage of a new function as of Mathematica 9.0, WhenEvent, which determines the loci of the azeotropes; indeed they verify
is given in a separate plot. In both cases, the azeotrope disappears at a low enough total pressure. One particular feature of the present calculation is that it uses the arc length continuation method (see the Details section) to find the bubble/dew point temperatures versus liquid/vapor phase compositions. This takes advantage of a new function as of Mathematica 9.0, WhenEvent, which determines the loci of the azeotropes; indeed they verify 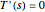 , where
, where  is the arc length parameter.
is the arc length parameter.
Contributed by: Housam Binous, Ahmed Bellagi, and Brian G. Higgins (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For vapor-liquid equilibrium data computations, the nonlinear equation  , where
, where  is the liquid mole fraction and
is the liquid mole fraction and  is the bubble temperature, is the bubble point equation derived from Dalton's law and the modified Raoult's law. Introduce an arc length parameter
is the bubble temperature, is the bubble point equation derived from Dalton's law and the modified Raoult's law. Introduce an arc length parameter  . The nonlinear algebraic equation becomes
. The nonlinear algebraic equation becomes 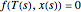 . We use the built-in Mathematica function NDSolve to solve this equation together with the differential equation (called the arc length constraint)
. We use the built-in Mathematica function NDSolve to solve this equation together with the differential equation (called the arc length constraint) 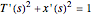 in order to find
in order to find  and
and 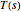 . A simple initial condition is found by taking
. A simple initial condition is found by taking  and
and  equal to the boiling temperature of pure ethanol at
equal to the boiling temperature of pure ethanol at  .
.
Permanent Citation