Weissenberg Effect in Ferrofluids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
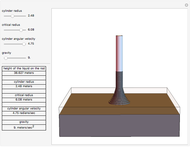
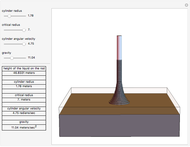
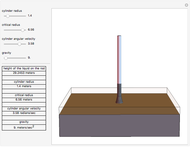
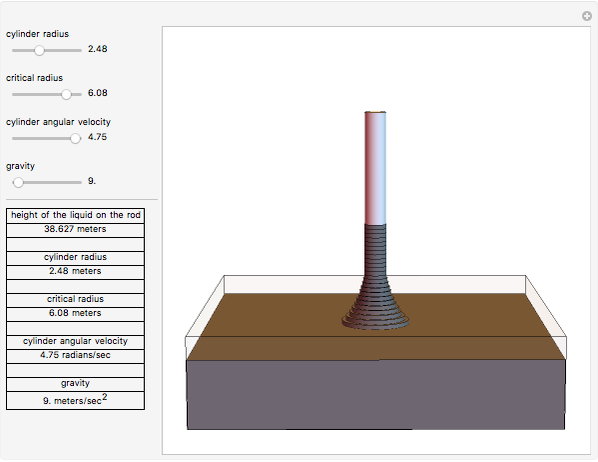
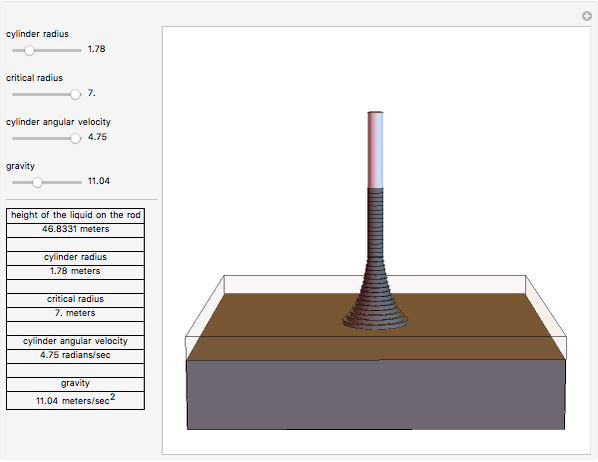
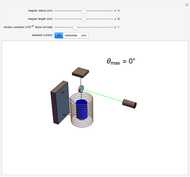
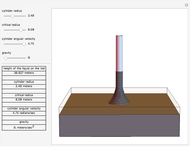
In the Weissenberg effect, a non-Newtonian fluid tends to climb up the walls of a spinning rod. This effect is usually illustrated by a ferrofluid (magnetic fluid), as in this Demonstration. Rotating a rod in a ferrofluid above some critical angular velocity exhibits this phenomenon.
[more]
Contributed by: Vighnesh Souda (January 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equation for the Weissenberg effect is

 ,
,
where  is the height that the liquid will reach on the rod,
is the height that the liquid will reach on the rod,  is the radius of the rod, ω is the angular velocity of the rod,
is the radius of the rod, ω is the angular velocity of the rod,  is the gravitational acceleration, and
is the gravitational acceleration, and  is the critical radius.
is the critical radius.
References
[1] W. S. Harvie. "AP Physics C Notes." (Jan 20, 2015) teachers.sduhsd.net/tpscience/physics/notes/AP Physics C Notes - Mechanics/118 - 161 Rotations.pdf.
[2] S. Odenbach, T. Rylewicz, and H. Rath, "Investigation of the Weissenberg Effect in Suspensions of Magnetic Nanoparticles," Physics of Fluids, 11(10), 1999 p. 2901. doi:10.1063/1.870148.
Permanent Citation