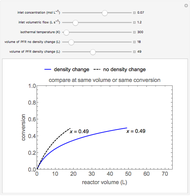
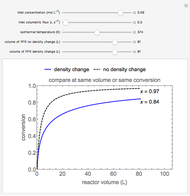
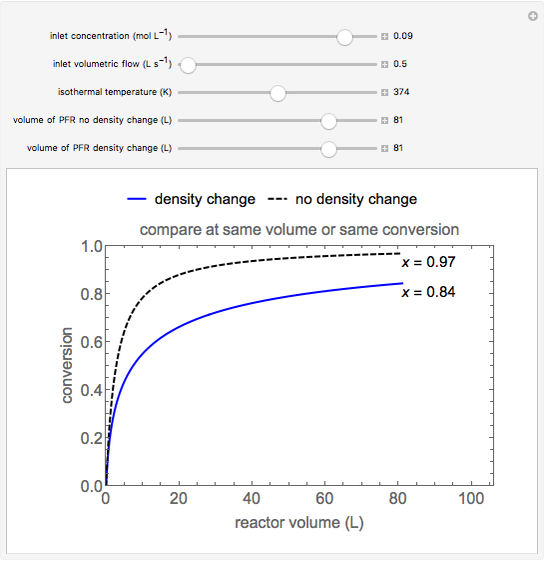
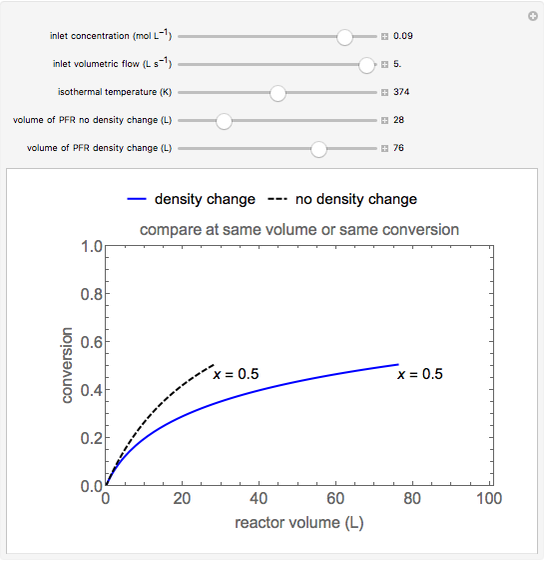
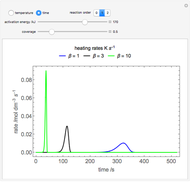
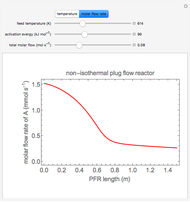
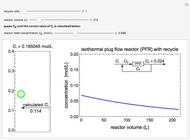
This Demonstration calculates conversion as a function of reactor volume for a second-order, gas-phase reaction in an isothermal, isobaric, plug flow reactor (PFR). The number of moles increases as conversion increases for the reaction , and this causes the mass density to decrease. Thus, the volumetric flow rate increases down the reactor so that the conversion (blue line) is lower than what would be obtained if the mass density were assumed constant (dashed green line). A higher volumetric flow rate means a shorter residence time. Use sliders to change the volumes of the reactor with and without density change in order to make comparisons at the same conversion or the same reactor volume. Use sliders to change the feed reactant concentration, feed volumetric flow rate, and reactor temperature.