Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Chemical Equilibrium in the Haber Process

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

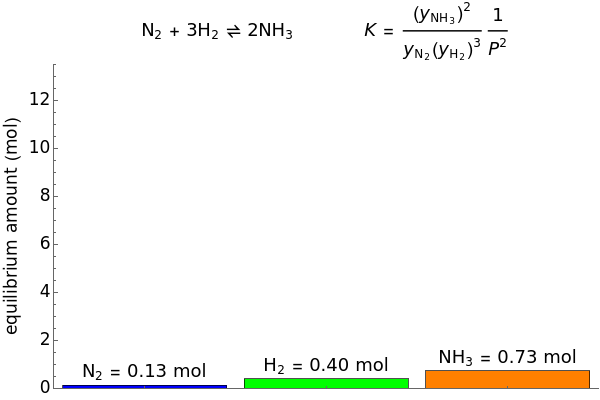
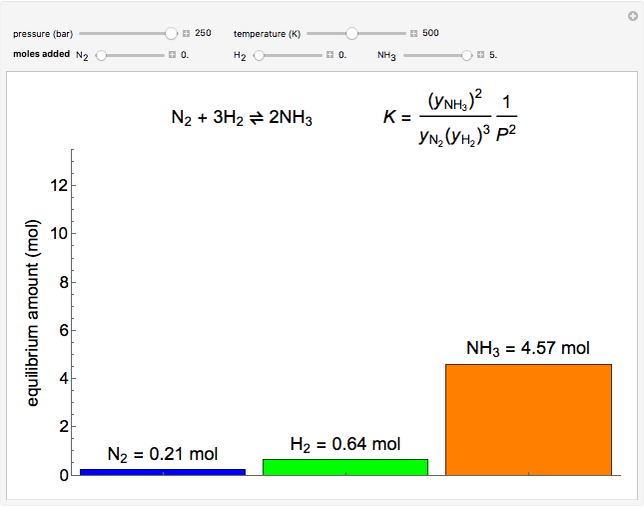
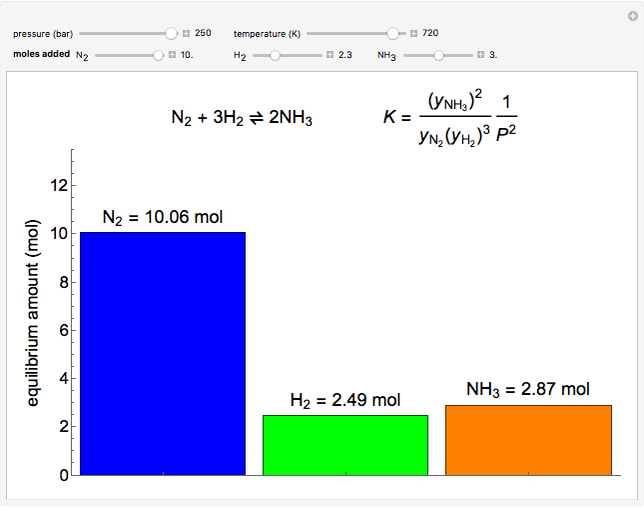
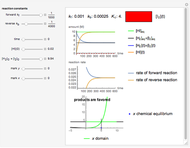
This Demonstration calculates the number of moles at equilibrium for the reversible, exothermic reaction that synthesizes ammonia () from hydrogen () and nitrogen (), known as the Haber process. This reaction typically takes place near 200 bar and 675 to 725 K. The system starts with 1 mol and goes to equilibrium. Use sliders to add additional moles of , and at constant pressure and temperature and observe how they change equilibrium. Vary pressure and temperature with sliders. Because 4 mol of reactants form 2 mol of product, raising the pressure shifts equilibrium toward products. Gases are assumed ideal, but at the high pressures used for this reaction, significant deviation from ideal behavior is likely.

[more]

Le Chatelier's principle predicts that when moles of or are added, reaction shifts to the right, whereas adding shifts the reaction to the left. However, when the ratio is sufficiently high, adding shifts reaction to the left (i.e., adding increases the amount of ), contrary to Le Chatelier's principle. This happens because adding when the ratio is high decreases the mole fraction, and because the mole fraction is cubed in the equilibrium expression, reacts to increase the number of moles of and .

[less]

Contributed by: Benjamin L. Kee and Rachael L. Baumann (May 2014)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA

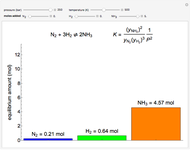
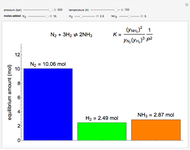
Snapshots

Details

The reaction is used in the Haber process. The moles of each component at equilibrium is:

,

where are the moles of component added, is the stoichiometric coefficient and is extent of reaction (mol). Initially only 1 mol is present.

The mole fraction at equilibrium is:

,

,

where is the total number of moles.

The extent of reaction is found by setting the equilibrium constant equal to the equilibrium rate constant and solving for :

,

,

where is Gibbs free energy (J/mol), is the heat of reaction (J/mol), is the entropy change of reaction (J/(mol K)), is temperature (K), is the ideal gas constant (J/(mol K)) and is pressure (bar).

The screencast video at [1] shows how to use this Demonstration. The screencast at [2] show solutions of an example problem on gas phase equilibrium.

References

[1] Chemical Equilibrium in the Haber Process [Video]. (Jan 20, 2017) www.colorado.edu/learncheme/thermodynamics/HaberProcess.html.

[2] Gas Phase Chemical Equilibrium [Video]. (Jan 20, 2017) www.youtube.com/watch?v=3ArBH_gbsNw.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send