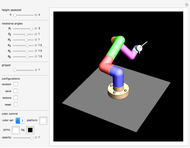
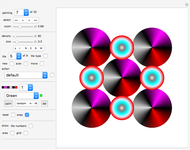
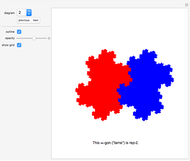
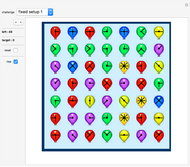
3D Curve Constructor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
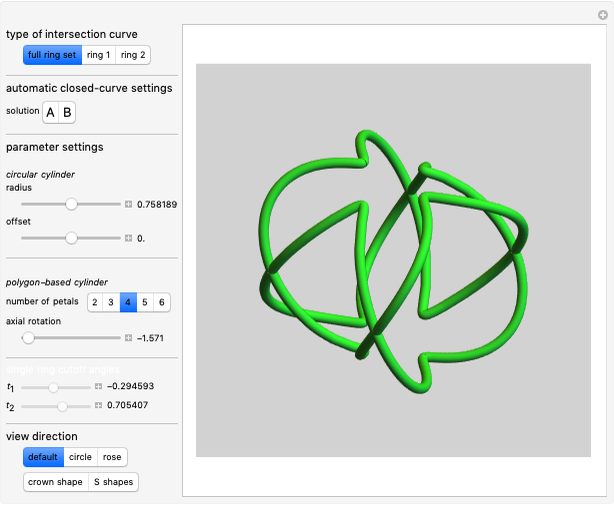
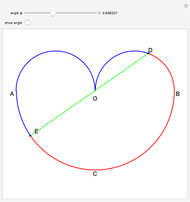
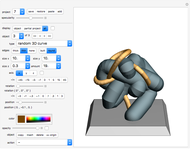
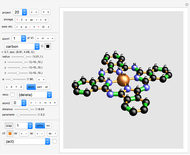
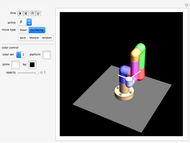
Create your own pieces of 3D art by bending a tube (of varying width, if desired) into any shape imaginable, or edit one of the designs given. You can display any number of curves in one image.
[more]
Contributed by: Karl Scherer (June 2011)
Open content licensed under CC BY-NC-SA
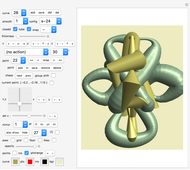
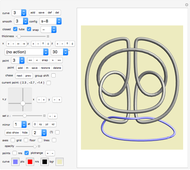
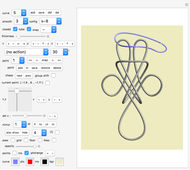
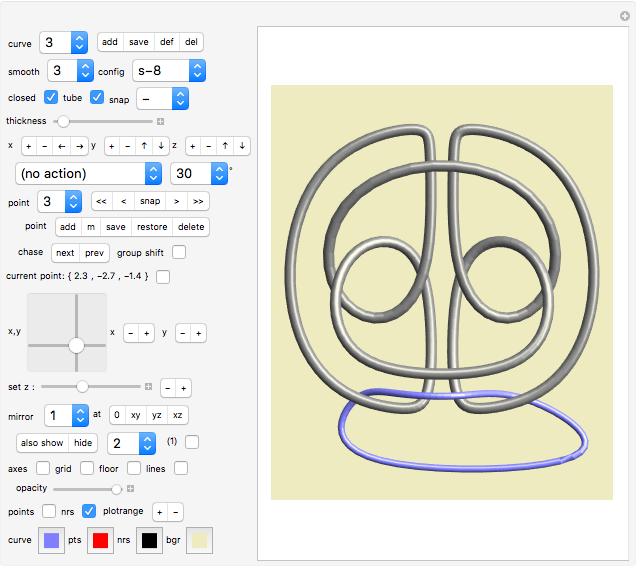
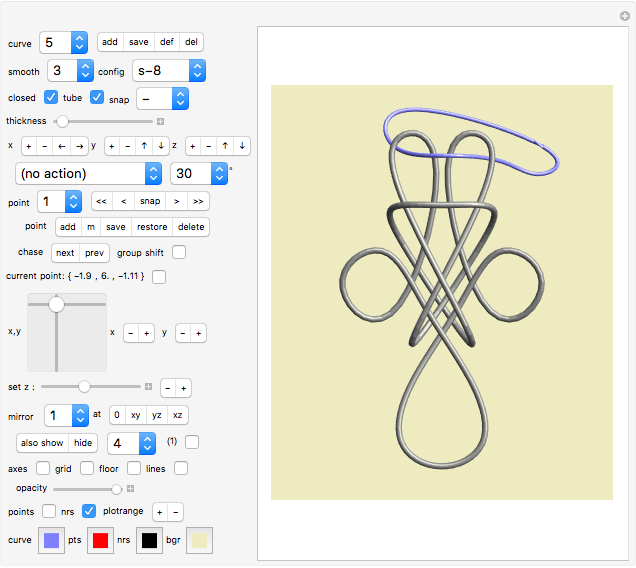
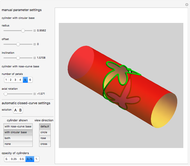
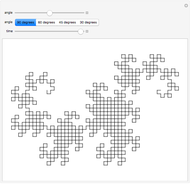
Snapshots
Details
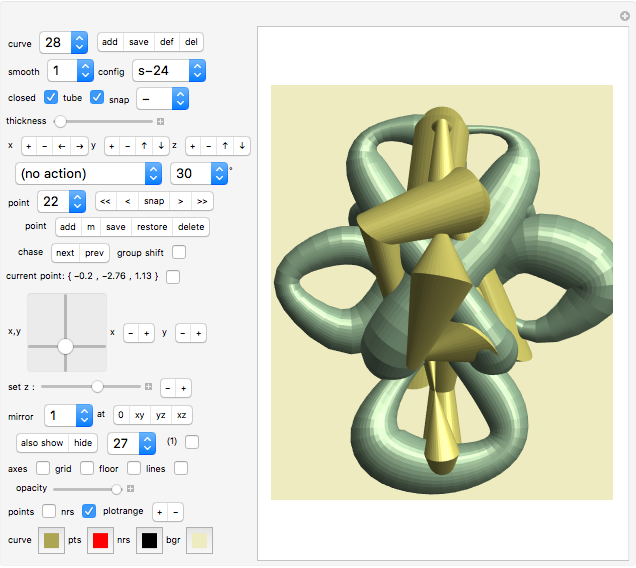
curve
Use this control to select the curve you would like to look at or edit.
add/save/def/del
Click the "add" button to add the currently edited curve as a new curve to your art collection.
Click the "save" button to save the current curve and associated data.
Click the "def" (default) button to recreate the original curve. If you added this curve, it will stay unchanged.
Click the "del" button to delete the currently edited curve.
smooth
Here you select the spline degree of your curve. The higher the degree, the smoother the curve.
config
Here you can select a standard (square or circular) starting configuration with 8, 16, 24, 32, or 40 control points. The entries "s-8", "s-16", "s-24", "s-32", and "s-40" denote the square configurations; the entries "o-8", "o-16", "o-24", "o-32", and "o-40" denote the circular configurations. There are also configurations named sp-nn and op-nn, which are square and round spirals (unselect the "closed" option and rotate the setup in 3D to see the spirals more clearly).
Please note that you can always add or delete control points later.
closed
Here you select whether your curve is a closed curve.
tube
This checkbox controls whether your curve will be displayed as a line or as a tube. Related control: "thickness".
snap
The snap modes will only affect the current control point's coordinates immediately after selecting the snap mode and also during manually changing the 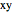 or
or  slider.
slider.
"snap 1" adjusts the currently edited control point to the nearest point with integral coordinates.
"snap .5" adjusts the coordinates of the currently edited control to the nearest multiples of .5 units.
"snap .25" adjusts the coordinates of the currently edited control to the nearest multiples of .25 units.
thickness
This slider controls the thickness of the curve (displayed as a thick line or a tube; see checkbox "tube" above).
If "tube" is active, then the slider only controls the thickness at the current point. To apply this thickness to all points use the action "equal thickness" (see below).
x +-.., y+-.., z+-.. setter bars
The first two buttons ("+","-") of each setter bar shrink (to 90%) or enlarge (to 110%) your curve's breadth, width, or height.
The other two buttons shift (by increments of .1) the whole curve in the  ,
, 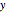 , or
, or  direction. If a snap mode is active, the increments are those associated with the snap mode (namely 1, .5, or .25 units).
direction. If a snap mode is active, the increments are those associated with the snap mode (namely 1, .5, or .25 units).
If "group shift" is active (see further down), then only some of the points are affected.
actions
"flip x" inverts the sign of the  coordinates of all control points.
coordinates of all control points.
"flip y" inverts the sign of the 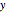 coordinates of all control points.
coordinates of all control points.
"flip z" inverts the sign of the  coordinates of all control points.
coordinates of all control points.
"mirror at origin" inverts the sign of the coordinates of all control points.
"rotate around x axis" rotates the whole curve around the  axis by the amount given in degrees.
axis by the amount given in degrees.
"around y axis" rotates the whole curve around the 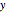 axis by the amount given in degrees.
axis by the amount given in degrees.
"rotate around z axis" rotates the whole curve around the  axis by the amount given in degrees.
axis by the amount given in degrees.
"snap all" snaps the coordinates of all control points (see description of "snap" popup menu above).
"renumber points" makes the currently edited control point the first control point and renumbers all others accordingly. This can be very useful when you want to cut a closed curve at any point, because the breaking point will always be between the last and first point.
"reverse sequence" reverses the sequence of the control points: the first point will become the last.
"straighten" creates a straight line of control points from the current control point to the point given in the "mirror" drop-down menu.
"flatten" sets the z-coordinates of all points to the same average value. If "groupshift" is active, not all points are affected.
"circle" computes the center of the curve and arranges all control points at the same distance around this center. If "groupshift" mode is active (see above), the circular procedure will only act on the given range of control points.
"split curve" cuts the current curve into two pieces. The first piece runs from the first control point to the point before the current one. The second piece starts at the currently edited control point. The second curve will be stored separately under a new curve number and cannot be edited on the current screen, but will still be visible as an "also show" entry, and will have its first point highlighted. The first curve part can still be edited.
"split curve, no gap" cuts the current curve into two pieces. The first piece runs from the first control point to the current point. The second piece starts at the current control point. The second curve will be stored separately under a new curve number and cannot be edited on the current screen, but will still be visible as an "also show" entry, and will have its first point highlighted. The first curve part can still be edited.
"join curves" joins the "also show" curve to the end of the currently edited curve. Hence "action = join curves" is the opposite of "action = split curves".
"shift to join" shifts a second ("also show") curve in such a way that its first control point is positioned exactly where the last control point of the current curve is. The curves are then joined by the system and the surplus duplicate point deleted. Hence "action = shift to join" is the opposite of "action = split, no gap".
"equal thickness" sets the tube thickness at all points to the thickness value of the current point.
"thickness from-to" takes the thicknesses at two points (the second point number given by the "mirror" pop-up menu) and interpolates the thickness between these two points.
"random thickness" randomizes the curve thickness so that is has a different thickness (between 0 and the current slider value) at each point. Hence set the thickness slider first to control the randomness.
"perturb curve" adds a percentage of each point's coordinates to the current coordinates. E.g., the number 30 next to the actions will cause a disturbance of up to 30 percent (up to 30*Max[x,y,z]/100) in any direction.
"light = Neutral/Automatic/None" gives you three lighting options.
"viewpoint = top/normal" gives you two options for the viewpoint, resulting in a view either straight from the top or more from the side.
point
Here you select the control point you want to edit. If the "current point" checkbox is active (see further down), the currently edited control point is marked by a large red dot; all other points are marked by a small red dot.
< />>
Click one of the <<,<,>,>> buttons to jump to the first, previous, next, or last control point.
Note that if you switch to another control point without clicking the "save" button first, (in general) the changes to the old control point will not be stored!
Click "snap" to snap the current point's coordinates to the grid (which has only an affect if the "snap size" is given). Note that there are three snap sizes available (snap = 1/.5/.25, see above). There is no "automatic" snap in this Demonstration!
add/m/save/restore/delete
Click "add" to double the current control point. The numbering of all other control points will be changed accordingly.
Click "m" to create a new point positioned midway between the current point and the next point.
Click "save" to store the position of the current control point and all other relevant data.
Click "restore" to restore the position of the current control point, but none of the other relevant data.
Click "delete" to delete the current control point.
"chase next/previous" setter bar
If "next" is clicked, the current control point is shifted halfway towards the next point in the sequence.
If "previous" is clicked, the current control point is shifted halfway towards the previous point in the sequence.
"group shift" toggle
"group shift" causes the x,y,z shift buttons (the arrows in +/-/←/) to act on only some of the curve control points, namely on all those from the current control point to the point given in "mirror". Similarly, action "perturb curve" will only perturb a part of the curve is "group shift" is active.
current point at: {x,y,z}
This displays the position of the currently edited control point (i.e., the vertex of the underlying polyline).
micro-manipulation checkbox (at end of "current point..." line)
Click it to put the 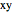 slider and the
slider and the  slider into micro-manipulation mode, in which they span only a distance of one unit in each direction.
slider into micro-manipulation mode, in which they span only a distance of one unit in each direction.
When you click the micro mode, the 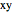 slider is set at
slider is set at 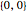 and the
and the  slider is set to zero. The two sliders now do not represent absolute coordinates anymore, but rather represent the coordinates around the position of your control point at the time when you chose to enter micro mode. If you now move the sliders you will see that they move slower, but give you much more control and precision for placing the control point.
slider is set to zero. The two sliders now do not represent absolute coordinates anymore, but rather represent the coordinates around the position of your control point at the time when you chose to enter micro mode. If you now move the sliders you will see that they move slower, but give you much more control and precision for placing the control point.
Important: During micro mode only the 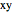 slider and the
slider and the  slider should be used. To go back to normal mode with all buttons available click the micro-manipulation checkbox again.
slider should be used. To go back to normal mode with all buttons available click the micro-manipulation checkbox again.
x,y 2D slider
Use this 2D slider to choose the  and
and 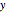 coordinates of the control point.
coordinates of the control point.
x -/+, y -/+
Click these controls to change the  or
or 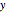 coordinate of the currently edited control point by .1 units.
coordinate of the currently edited control point by .1 units.
If "snap" is active, the increments are set accordingly (to 1, .5, or .25).
set z slider
Use this slider to position the current control point in the third dimension.
-/+
Click this control to change the  coordinate of the currently edited control point by .1 units. If "snap" is active, the increments are set accordingly (1, .5, or .25).
coordinate of the currently edited control point by .1 units. If "snap" is active, the increments are set accordingly (1, .5, or .25).
mirror ... at 0/xy/yz/xz
Use this control to shift the current control point such that it becomes the mirror image of another control point.
The mirroring plane is either the origin, the 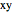 plane, the
plane, the 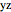 plane, or the
plane, or the 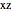 plane. E.g., the point mirrored at the
plane. E.g., the point mirrored at the 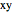 plane will simply be a copy of the referenced point with its
plane will simply be a copy of the referenced point with its  coordinate inverted (multiplied by
coordinate inverted (multiplied by 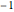 ).
).
also show/hide ... setter bar, selection popup menu, and show-list checkbox
In addition to the currently edited curve, you can display any number of additional already-completed curves.
Simply select the number of the curve to be shown from the associated popup menu, then click "also show". The additional curve will appear with its own thickness and color. This way the given examples manage to show the wire AND the string of the wire-and-string puzzles at the same time (see examples 3, 5, 7, etc.). The first point of the (last) additional curve will be marked by a black number "1" on a red dot.
The "hide" button will undo the display of a selected additional curve. (To temporarily hide the currently edited curve, set the thickness slider to zero.)
The number of additionally displayed curves is shown in round brackets.
Click the show-list checkbox to see an ordered list of additionally displayed curves; it will be displayed at the center bottom of the graphics display area. Also, large numbers on the graphics display area will indicate the first control point of each additional curve.
axes
Click this checkbox to show the coordinate axes.
grid
Click this checkbox to show a 6×6 grid in the 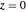 plane.
plane.
floor
Click this checkbox to show a 6×6 gray square (the floor) in the 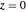 plane.
The opacity of the floor is fixed to .5 .
plane.
The opacity of the floor is fixed to .5 .
lines
Click this checkbox to show green lines connecting the series of control points.
opacity
This slider controls the opacity of the 3D curve.
points
Clicking this checkbox makes the control points appear/disappear.
If the checkbox is inactive, the numbers are not displayed (see "numbers" below).
If it is active (see further down), the currently edited control point is marked by a large red dot; all other points are marked by a small red dot.
If you cannot see the red dots, reduce the opacity of the tube or unselect "tube".
nrs
If the checkbox "points" is active, clicking the checkbox "numbers" displays/hides the sequence numbers of the control points. The number of the current point is blue, all others are black.
plotrange
Doubles (click "+") and halves (click "-") the plot range.
color swatches: curve, pts, nrs, bgr
Here you select the colors of the curve, the control points, the numbers, and the background.
Hints
• Click "point save" to store the position of the currently edited control point. You can "restore" the current control point to its previous value only after manually shifting or mirroring it. Most actions (like flipping the curve) will save the currently edited control point's position automatically.
• Clicking the "curve save" button at the top also stores all point-independent controls (such as "curve color"). So use this button regularly!
• When designing a 3D curve, it is often easier to create it in two dimensions (the 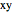 plane) first and add the third dimension (
plane) first and add the third dimension ( values) later. That is how the wire-and-string puzzles were implemented by the author.
values) later. That is how the wire-and-string puzzles were implemented by the author.
• To make sharp corners, use the same point twice in a row. If this makes the image disappear (happens when your curve is not closed and the current point is the first or last), move the twins slightly apart.
History
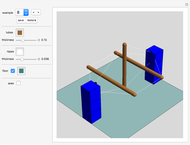
The examples provided are wire-and-string puzzles invented by the author in 1993. The task in these puzzles is to remove the closed string from the closed wire loop without cutting the string (the strings shown in the examples in this Demonstration are too short, of course; they just indicate where the long string is placed). The Demonstration "Wire-and-String Puzzles" by the same author lets you play with these puzzles, but the presentation of the puzzles is very simplified and does not show their nice three-dimensional, complex, and elegant curved design.
This led the author to use the technique of B-spline curves and to the idea of creating this general B-spline tool which lets you construct any combination of free-form 3D curves fast and easily.
Here is the list of wire-and-string puzzles included in this Demonstration, with example numbers:
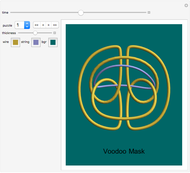
Voodoo Mask (2, 3)
King Arthur's Cross (4, 5)
Mystery Clover (6, 7)
Trapped Butterfly (8, 9)
Houdini's Dilemma (10, 11)
David's Star (easy) (12, 13)
David's Star (hard) (14, 15)
Double Heart (16, 17)
Racetrack (18, 19)
Sunglasses (20, 21)
Initials "AG" (22, 23)
The real wire-and-string puzzles are manually created from copper or steel wire. Silver plated and produced in small size, the first seven puzzles on the list are flat enough to be worn as pendants around your neck (puzzle jewelry).
Finally, examples number 24 and following show some more 3D curve designs.
Permanent Citation