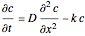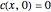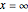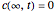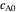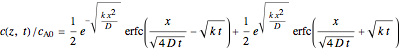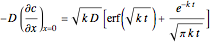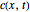Absorption with Chemical Reaction in a Semi-Infinite Medium

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
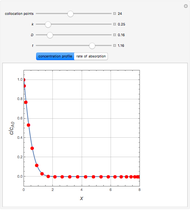
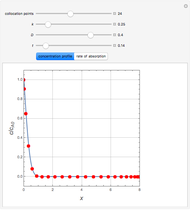
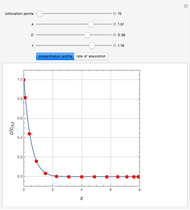
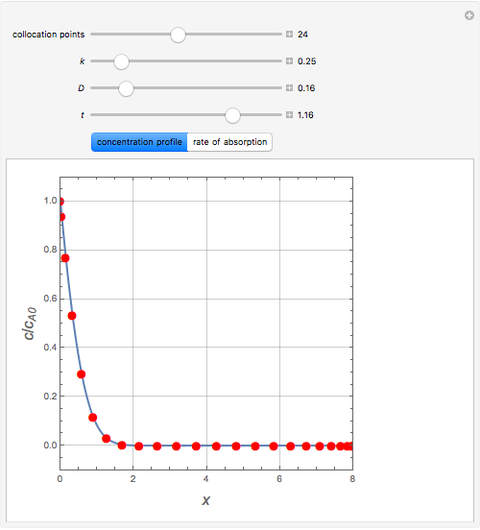
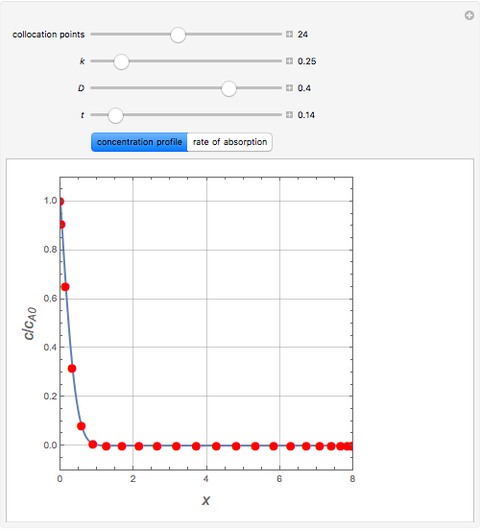
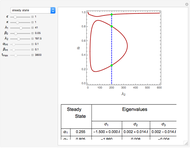
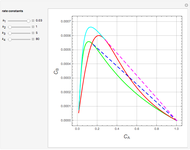
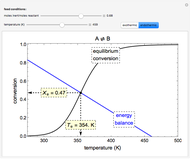
Consider the unsteady-state absorption with a chemical reaction in a semi-infinite medium. The governing equation is:
[more]
Contributed by: Housam Binousand Brian G. Higgins (June 2013)
Open content licensed under CC BY-NC-SA
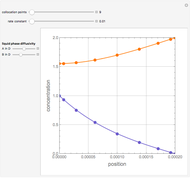
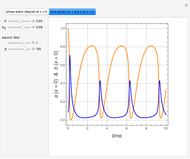
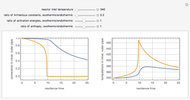
Snapshots
Details
In the discrete Chebyshev–Gauss–Lobatto case, the interior points are given by 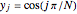 . These points are the extrema of the Chebyshev polynomials of the first kind,
. These points are the extrema of the Chebyshev polynomials of the first kind, 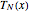 .
.
The 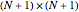 Chebyshev derivative matrix at the quadrature points is an
Chebyshev derivative matrix at the quadrature points is an 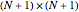 matrix
matrix 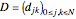 given by
given by
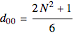 ,
, 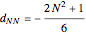 ,
, 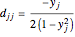 for
for  , and
, and 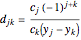 for
for  ,
, 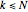 , and
, and 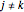 ,
,
where  for
for  and
and  .
.
The matrix  is then used as follows:
is then used as follows: 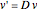 and
and  , where
, where  is a vector formed by evaluating
is a vector formed by evaluating  at
at 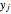 ,
, 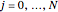 , and
, and 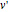 and
and  are the approximations of
are the approximations of 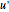 and
and  at the
at the 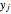 .
.
References
[1] P. Moin, Fundamentals of Engineering Numerical Analysis, Cambridge, UK: Cambridge University Press, 2001.
[2] L. N. Trefethen, Spectral Methods in MATLAB, Philadelphia: SIAM, 2000.
[3] R. B. Bird, W. E. Stewart, and E. N. Lightfoot, Transport Phenomena, 2nd ed., New York: John Wiley & Sons, 2002.
[4] P. V. Danckwerts, "Absorption by Simultaneous Diffusion and Chemical Reaction," Transactions of the Faraday Society, 46, 1950 pp. 300–304. doi:10.1039/TF9504600300.
Permanent Citation