Reversible Reaction in an Adiabatic Plug-Flow Reactor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
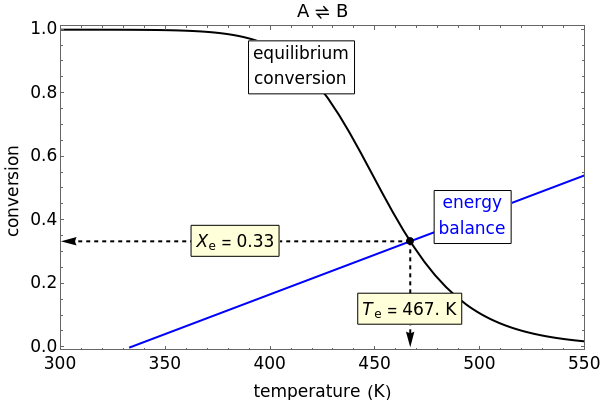
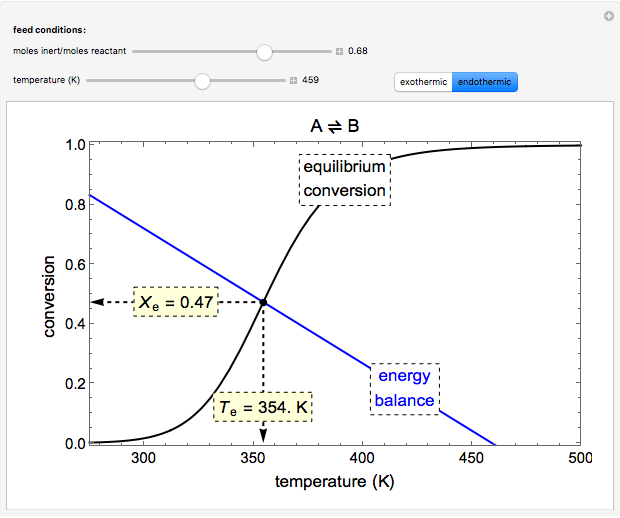
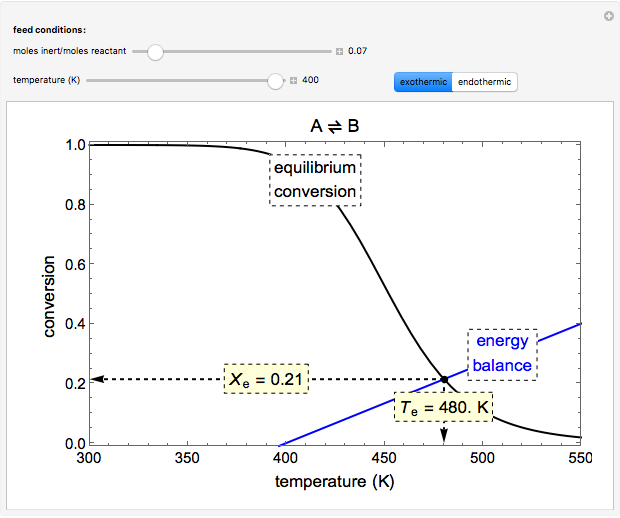
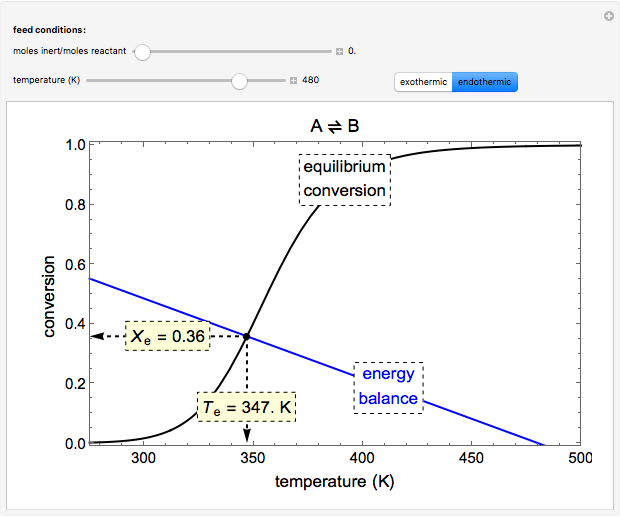
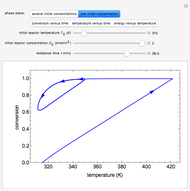
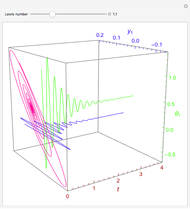
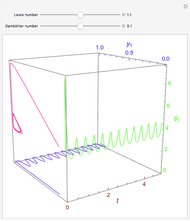
A reversible reaction, 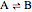 , takes place in an adiabatic plug-flow reactor (PFR). Select either an exothermic (
, takes place in an adiabatic plug-flow reactor (PFR). Select either an exothermic (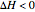 ) or an endothermic (
) or an endothermic (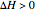 ) reaction. The black curve is the equilibrium conversion as a function of temperature from the van't Hoff equation. The blue line is conversion as a function of temperature from the adiabatic energy balance. The intersection of the curve and the line is the conversion at equilibrium (
) reaction. The black curve is the equilibrium conversion as a function of temperature from the van't Hoff equation. The blue line is conversion as a function of temperature from the adiabatic energy balance. The intersection of the curve and the line is the conversion at equilibrium ( ) and the adiabatic temperature at equilibrium (
) and the adiabatic temperature at equilibrium ( ). You can vary the feed temperature and the molar ratio of inert to reactant in the feed.
). You can vary the feed temperature and the molar ratio of inert to reactant in the feed.
Contributed by: Rachael L. Baumann (April 2015)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the reversible reaction 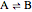 with both reactant
with both reactant 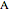 and inert component
and inert component 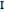 in the adiabatic PFR feed, the equilibrium constant is:
in the adiabatic PFR feed, the equilibrium constant is:
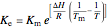 ,
,
where 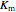 is the equilibrium constant at temperature
is the equilibrium constant at temperature 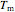 (K),
(K),  is the heat of reaction (J/mol),
is the heat of reaction (J/mol), 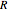 is the ideal gas constant (J/[mol K]), and
is the ideal gas constant (J/[mol K]), and 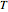 is the temperature of the reaction (K).
is the temperature of the reaction (K).
The equilibrium conversion is obtained from the equilibrium constant, assuming ideal gases:
 ,
,
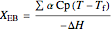 ,
,
where  is the equilibrium conversion,
is the equilibrium conversion, 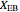 is the conversion calculated from the energy balance,
is the conversion calculated from the energy balance,  is the ratio in the feed of total mols/mols of reactant,
is the ratio in the feed of total mols/mols of reactant,  is the heat capacity (J/[mol K]) of both the reactant and the inert, and
is the heat capacity (J/[mol K]) of both the reactant and the inert, and  is the feed temperature (K).
is the feed temperature (K).
The screencast video at [2] explains how to use this Demonstration.
References
[1] H. S. Fogler, Essentials of Chemical Reaction Engineering, Upper Saddle River, NJ: Prentice Hall, 2011 pp. 503–505.
[2] Reversible Reaction in an Adiabatic Plug-Flow Reactor. www.colorado.edu/learncheme/thermodynamics/ReversibleReactionAdiabaticPFR.html.
Permanent Citation