An Example of Three-Dimensional Chaos
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
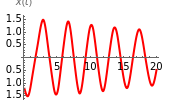
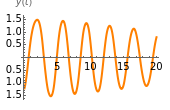
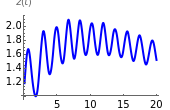
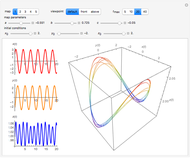
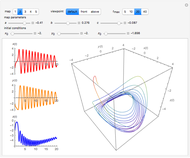
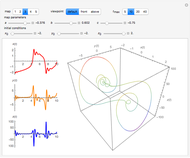
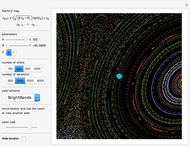
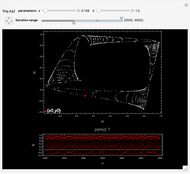
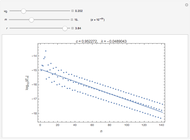
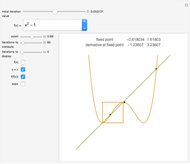
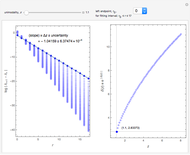
This Demonstration illustrates the periodic or chaotic behavior and the sensitivity to initial conditions of three-dimensional maps of the form:
[more]
Contributed by: Erik Mahieu (December 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The systems considered here are as follows:
map 1: 

map 2: 
map 3 (Rössler): 
map 4: 
map 5 (Lorentz): 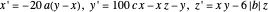
Reference
[1] J. L. Casti, "Order in Chaos," chap. 4 in Reality Rules: I, New York: John Wiley & Sons, 1992 p. 355. books.google.com/books/about/Reality_rules.html?id=nPQIuVYBjBQC.
Permanent Citation