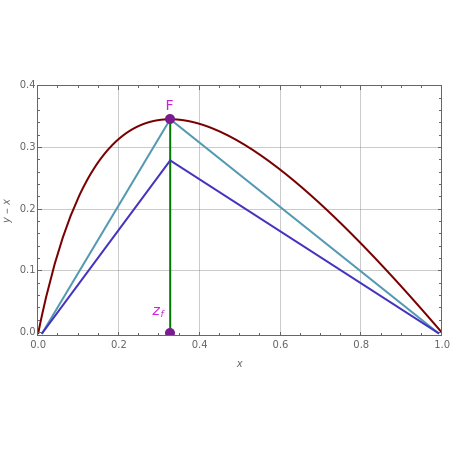
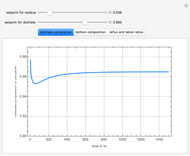
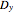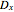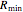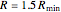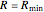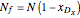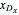The driving-force diagram for a constant relative volatility binary mixture is obtained by plotting 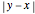 versus
versus  , where
, where  and
and 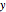 are the liquid and vapor mole fractions of the light component. Explicitly, the driving force is
are the liquid and vapor mole fractions of the light component. Explicitly, the driving force is 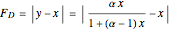 , where
, where  is the relative volatility.
is the relative volatility.
Two case are treated in the present Demonstration.
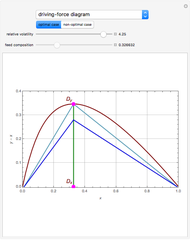
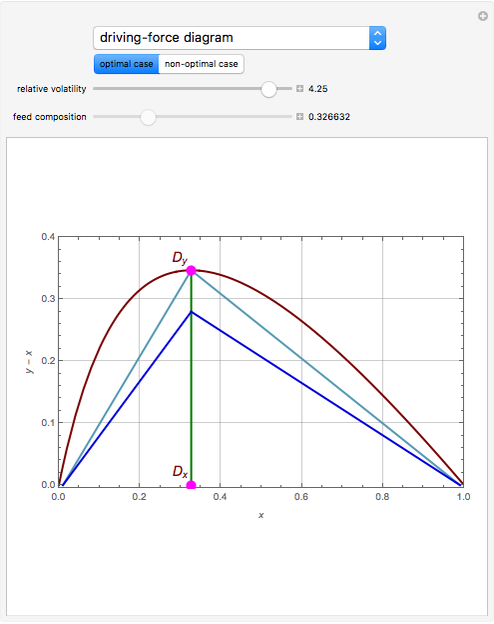
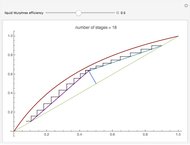
Optimal case: The curve obtained is concave and one can easily find the location of the maximum point (i.e. magenta point 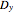 ). Let us take a saturated liquid feed with a composition given by the abscissa of the magenta point
). Let us take a saturated liquid feed with a composition given by the abscissa of the magenta point 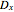 . The line
. The line  is the locus of the points of intersections for the operating lines corresponding to the largest actual driving force. Thus, if the feed plate is located on the line
is the locus of the points of intersections for the operating lines corresponding to the largest actual driving force. Thus, if the feed plate is located on the line  , the resulting design will minimize the operating cost of the distillation column (it simultaneously minimizes the reboil and reflux ratios). If the reflux ratio is equal to
, the resulting design will minimize the operating cost of the distillation column (it simultaneously minimizes the reboil and reflux ratios). If the reflux ratio is equal to 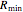 , then the operating lines, shown in light blue, intersect at
, then the operating lines, shown in light blue, intersect at 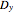 . The slope of the two light blue lines are identical, which means that the minimum reflux and reboil ratios are equal. For
. The slope of the two light blue lines are identical, which means that the minimum reflux and reboil ratios are equal. For 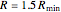 , the operating lines are drawn in blue. The slope of the operating lines in the driving-force diagram can be easily related to the reboil and reflux ratios. If these operating lines intersect exactly at
, the operating lines are drawn in blue. The slope of the operating lines in the driving-force diagram can be easily related to the reboil and reflux ratios. If these operating lines intersect exactly at 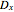 , then their slope is zero and we have the total reflux situation—this corresponds to operating lines in the McCabe–Thiele diagram given by the line
, then their slope is zero and we have the total reflux situation—this corresponds to operating lines in the McCabe–Thiele diagram given by the line  .
.
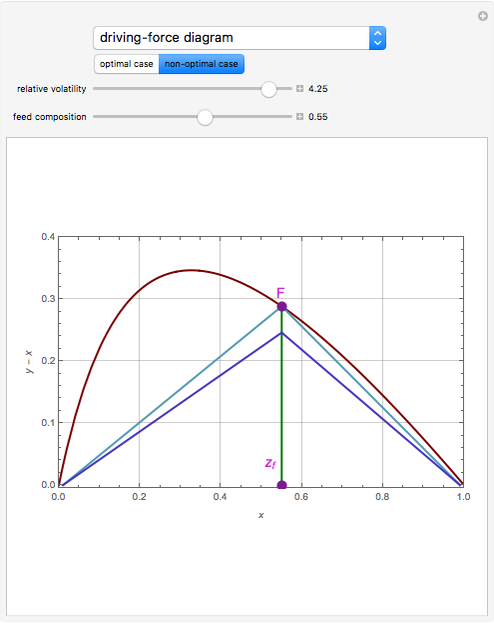
Non-optimal case: Let us take a saturated liquid feed with a composition,  , to be set by the user. If the reflux ratio is equal to
, to be set by the user. If the reflux ratio is equal to 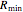 , then the operating lines, shown in light blue, intersect at
, then the operating lines, shown in light blue, intersect at  . For
. For 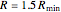 , the operating lines are drawn in blue. The slope of the operating lines in the driving-force diagram can be easily related to the reboil and reflux ratios.
, the operating lines are drawn in blue. The slope of the operating lines in the driving-force diagram can be easily related to the reboil and reflux ratios.
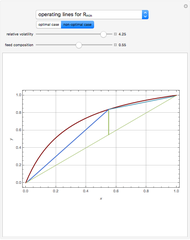
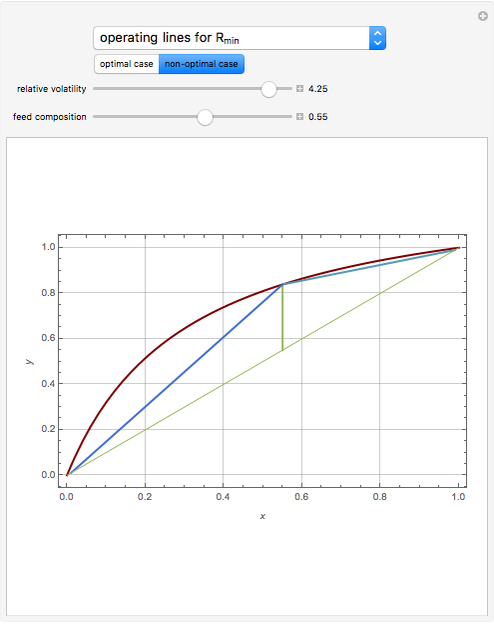
This Demonstration plots the driving-force diagram, the operating lines for 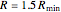 and
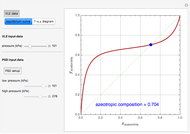
and 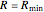 . You can change the value of the relative volatility of the mixture. The McCabe–Thiele diagram is also given. Finally, the minimum reflux ratio is computed in the program by two methods: (1) using the intersection of the feed line and the equilibrium curve, which is the classical McCabe–Thiele method, and (2) using the slope of the light blue operating lines in the driving-force diagram. Both methods give the same result for the minimum reflux ratio.
. You can change the value of the relative volatility of the mixture. The McCabe–Thiele diagram is also given. Finally, the minimum reflux ratio is computed in the program by two methods: (1) using the intersection of the feed line and the equilibrium curve, which is the classical McCabe–Thiele method, and (2) using the slope of the light blue operating lines in the driving-force diagram. Both methods give the same result for the minimum reflux ratio.
Finally, for the optimal case, the optimal feed location is calculated using the McCabe–Thiele diagram as well as the driving-force diagram. For the later approach, one has the following relationship: 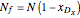 , where the stages are counted from the top and
, where the stages are counted from the top and 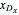 is the abscissa of
is the abscissa of 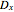 .
.
For lower values of  , the value of
, the value of 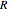 will be higher. Indeed, the separating driving force is smaller and the cost of the distillation will go up.
will be higher. Indeed, the separating driving force is smaller and the cost of the distillation will go up.
In this Demonstration, it is assumed that distillate and bottom specifications are  and
and 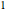 mole %, respectively
mole %, respectively
[less]

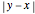 versus
versus  , where
, where  and
and 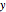 are the liquid and vapor mole fractions of the light component. Explicitly, the driving force is
are the liquid and vapor mole fractions of the light component. Explicitly, the driving force is 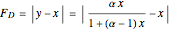 , where
, where  is the relative volatility.
is the relative volatility.