Details

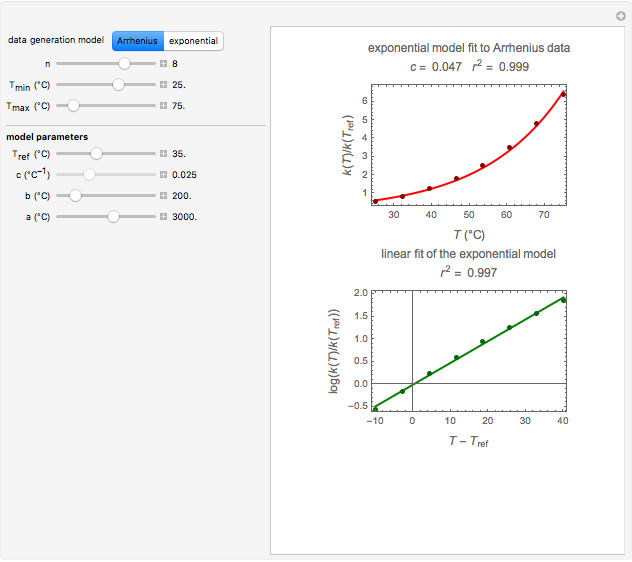
Snapshot 1: data generated with an Arrhenius-like equation where the absolute temperature reciprocal is replaced by 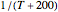and then fitted with the exponential model

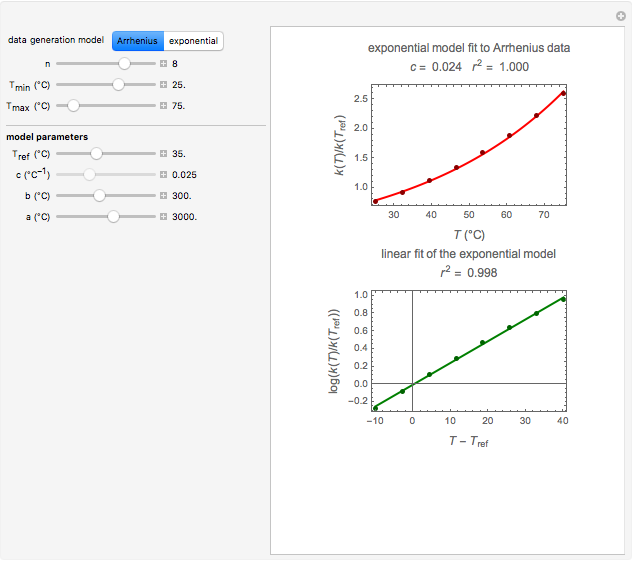
Snapshot 2: data generated with an Arrhenius-like equation where the absolute temperature reciprocal is replaced by 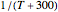and then fitted with the exponential model

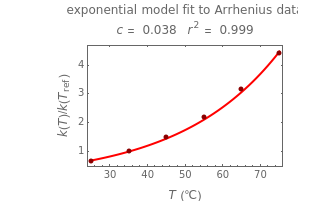
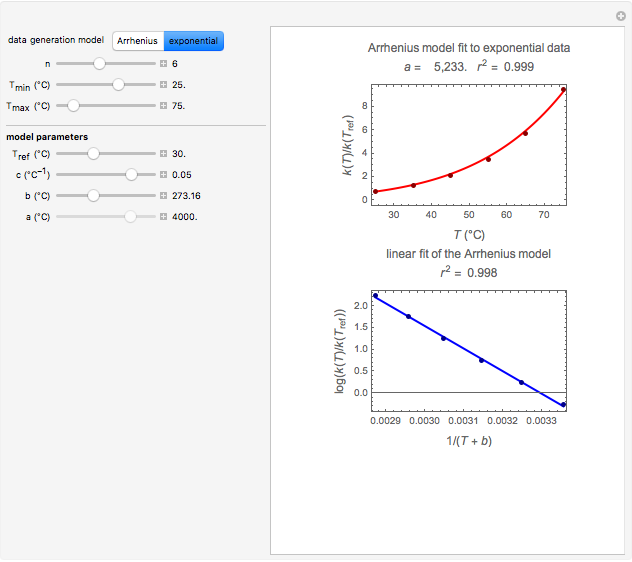
Snapshot 3: data generated with the exponential model and fitted with the standard Arrhenius equation (notice the linearity of the Arrhenius plot in blue)

Snapshot 4: data generated with the exponential model and fitted with an Arrhenius-like equation where the absolute temperature reciprocal is replaced by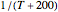

Snapshot 5: data generated with the exponential model and fitted with an Arrhenius-like equation where the absolute temperature reciprocal is replaced by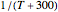

This Demonstration generates 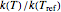versus 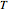datasets using the Arrhenius or Arrhenius-like equations that are fitted with an exponential model. It also generates such datasets using the exponential model that are fitted by the Arrhenius or Arrhenius-like equations. The Arrhenius-like equation is presented as 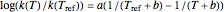, where 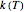and 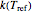are the rates at temperature 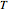and the reference temperature, 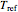, respectively, both in °C, and and are constants having temperature dimension. Notice that setting to 273.16 °C produces the standard Arrhenius equation. The exponential model equation is 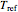) where is a constant having temperature reciprocal units (°).

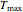The user chooses the data generation model by clicking the setter bar. The data so generated will be fitted by the other model. The number of points, , the plot's temperature range, and , the reference temperature, 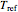, and the generation or fit parameters , , and , are entered with sliders.

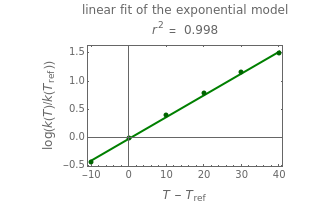
The display includes the generated 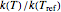versus 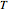data and their fit by the opposite model (top plot) and the 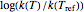versus 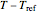or data fitted by the opposite model (bottom plot).

Notice that when is large, the Arrhenius plot of the data generated by the exponential model (blue dots in bottom plot) is almost perfectly linear regardless of its absolute magnitude.

All curves generated by the Arrhenius equation change concavity at a high enough temperature. When the generated data has downward concavity at the chosen settings, the Demonstration forgoes the fitting by the exponential model and displays a message to that effect.