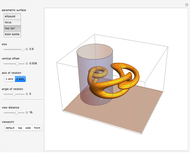
Circular Hole Drilled in a Cylinder

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
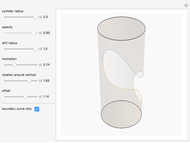
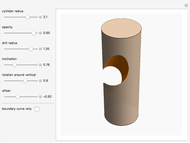
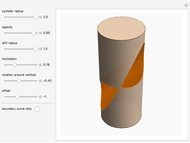
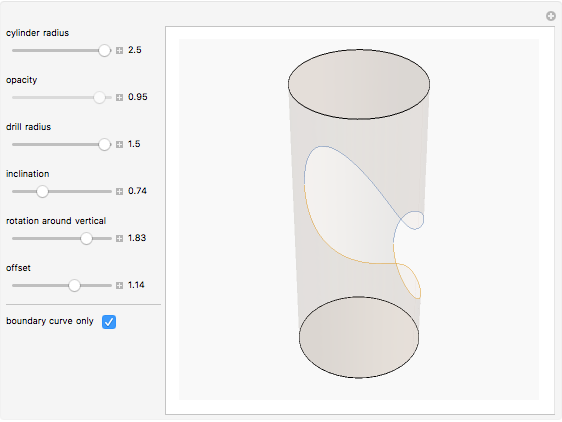
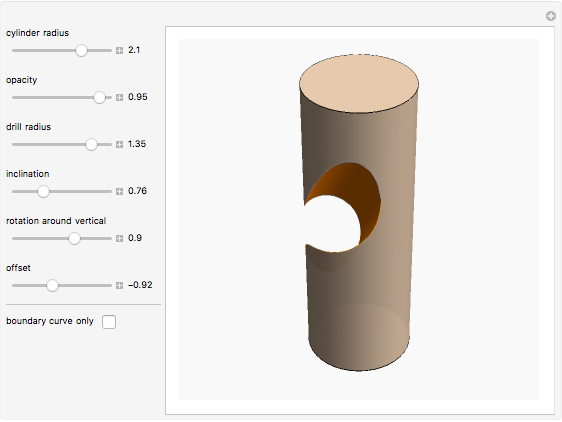
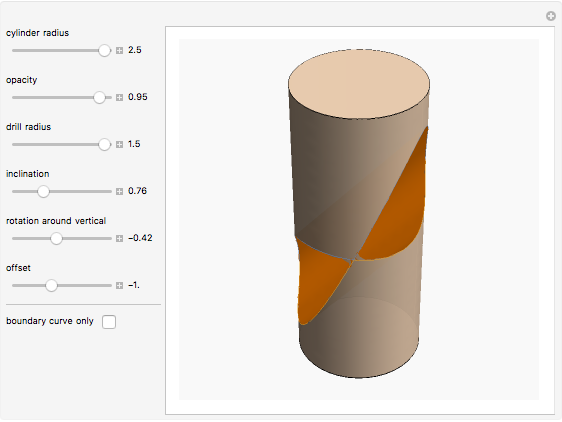
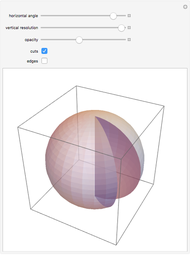
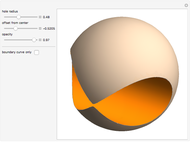
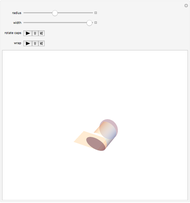
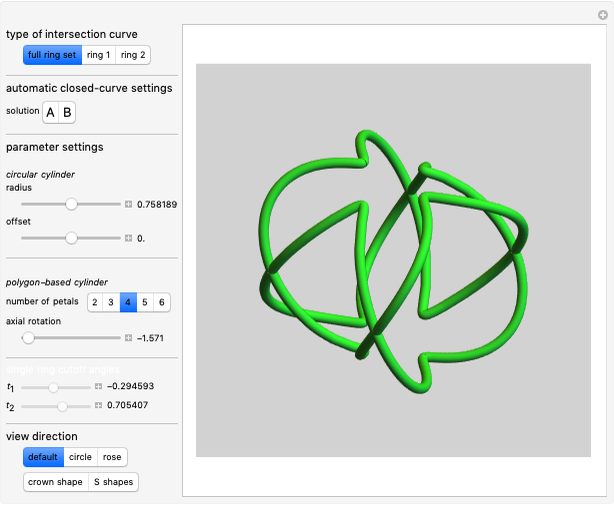
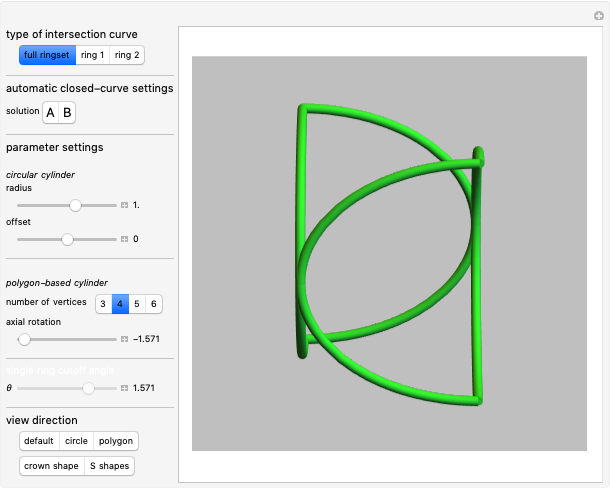
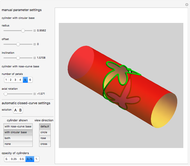
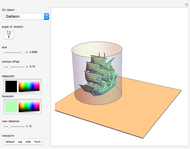
This Demonstration explores the shape of the difference between a cylinder and a circular cylinder.
Contributed by: Erik Mahieu (February 2014)
Open content licensed under CC BY-NC-SA
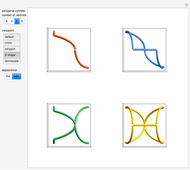
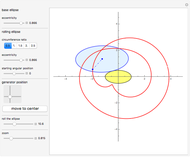
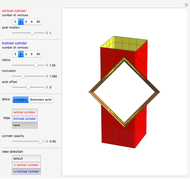
Snapshots
Details
Consider a cylinder of radius 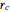 with axis parallel to the
with axis parallel to the  axis. Its parametric equations are
axis. Its parametric equations are
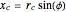 ,
,
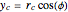 ,
,
 ,
,
where  and
and  are parameters.
are parameters.
Consider another cylinder, of radius 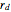 with axis at a distance
with axis at a distance  from the
from the  axis and where
axis and where  is the angle between the axis of the drill and the vertical. Its parametric equations are
is the angle between the axis of the drill and the vertical. Its parametric equations are
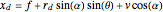 ,
,
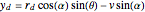 ,
,
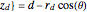 ,
,
where  and
and  are parameters.
are parameters.
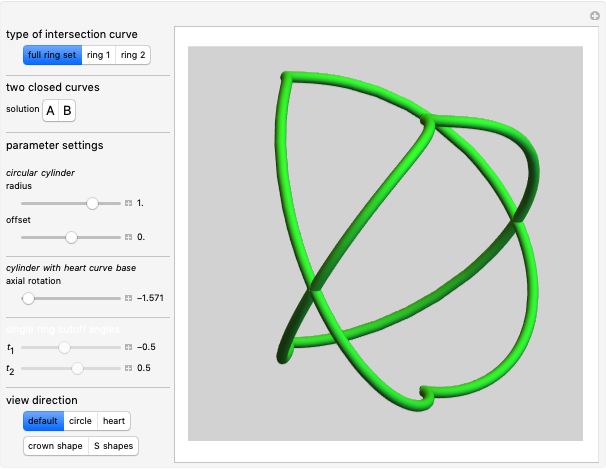
The intersection curve of the two surfaces can be obtained by solving the system of three equations

for three of the four parameters 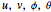 .
.
Solving for  ,
,  , and
, and  gives the parametric equations for the intersection curve with parameter
gives the parametric equations for the intersection curve with parameter  :
:
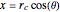 ,
,
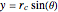 ,
,
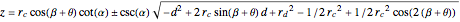
The two parts of the equation represent the upper and lower half of the intersection curve.
Permanent Citation