Circular Mass Accelerator

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
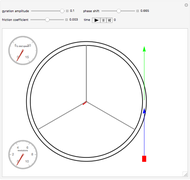
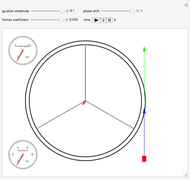
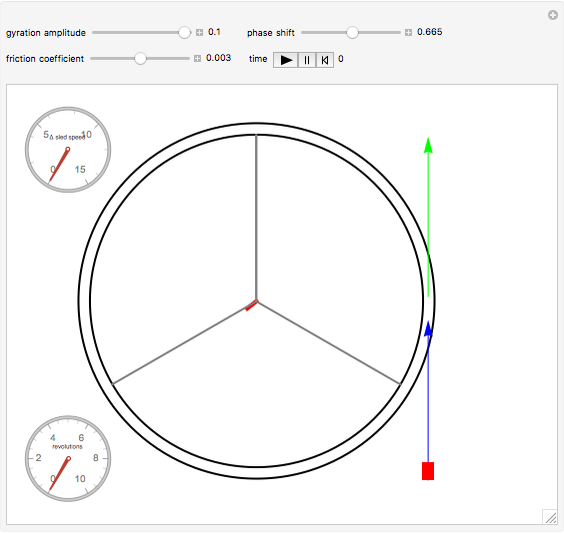
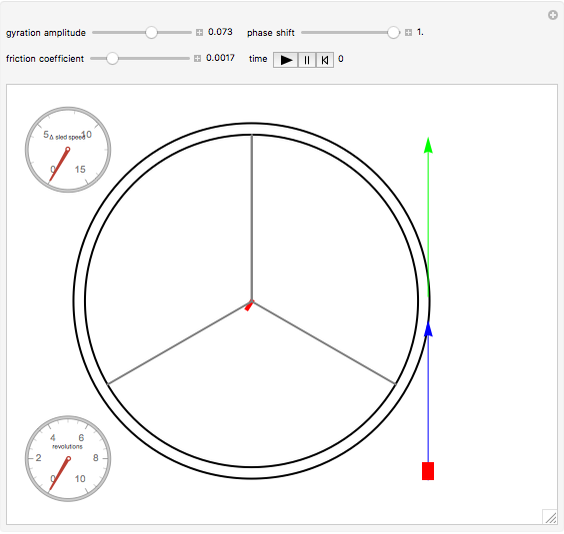
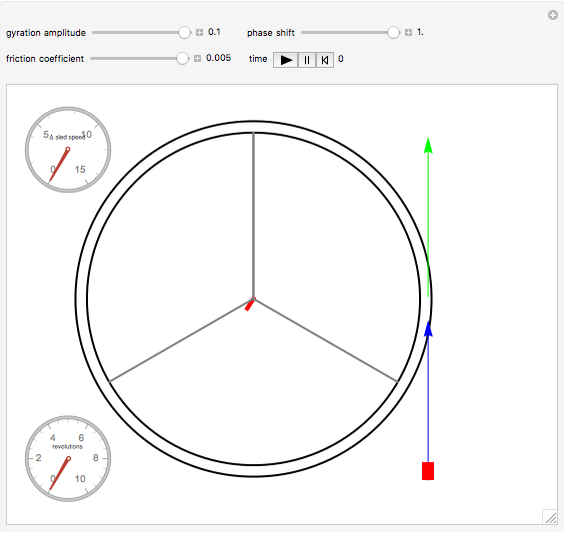
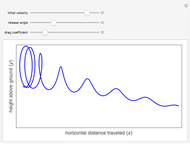
This Demonstration is a simulation of a circular mass accelerator based on the principle of the hula hoop [1].
[more]
Contributed by: Erik Mahieu (August 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A sled slides with a friction coefficient  at angular position
at angular position  inside a ring of radius
inside a ring of radius 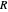 gyrating with eccentricity
gyrating with eccentricity  .
.
Gravity is neglected, as it is relatively small. From the equilibrium of centripetal and frictional forces acting on the sled and the geometry of the mechanism, the equation of motion [1, 2] is 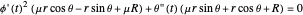 .
.
The values for 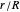 ,
,  , and
, and  being very small, the equation can be simplified to
being very small, the equation can be simplified to 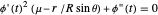 .
.
This ODE can now be solved symbolically to give 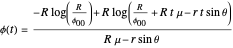 .
.
This Demonstration only gives a qualitative simulation of a mass accelerator. To see details about a real project (the Slingatron) see [3] and [4].
References
[1] A. O. Belyakov and A. P. Seyranian. "Regular Dynamics of a Hula-Hoop." istina.msu.ru/media/publications/articles/1bf/e6e/458523/Belyakov_A_O.pdf.
[2] D. A. Tidman, Slingatron—A Mechanical Hypervelocity Mass Accelerator, Sandy, UT: Aardvark Global Publishing, 2007. www.amazon.com/Slingatron-Mechanical-Hypervelocity-Mass-Accelerator/dp/1427626588.
[3] D. A. Tidman and F. D. Witherspoon, "Slingatron—A Mechanical Hypervelocity Sling," presentation given at Capital Science Conference (CSC 2008), Washington, DC. www.washacadsci.org/activities-and-events/capsci-abstracts/capital-science-2008/#tidman.
[4] A. Nowicki. "Slingatron with Magnetic Bearing." (Sept 23, 2006) www.islandone.org/LEOBiblio/SPBI125.HTM.
http://www.washacadsci.org/capsci08/presentations/ASTI-tidman.pdf
Permanent Citation