Constructing Voronoi Diagrams with Expanding Cells

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
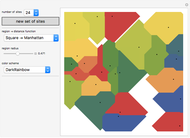
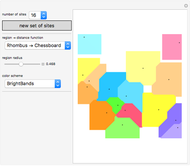
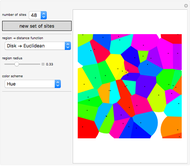
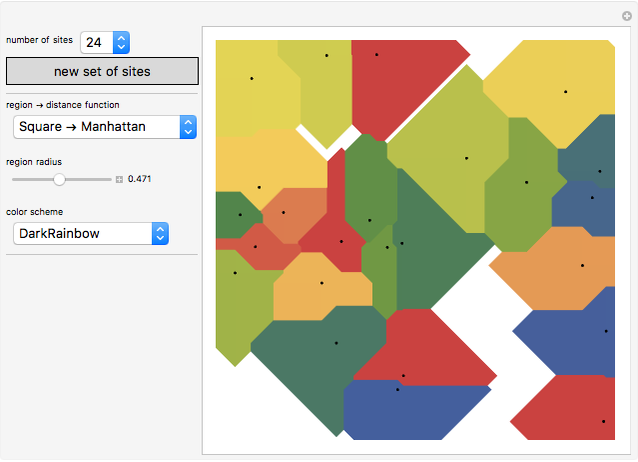
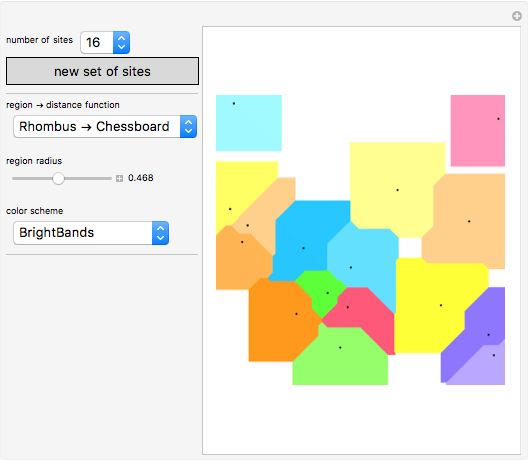
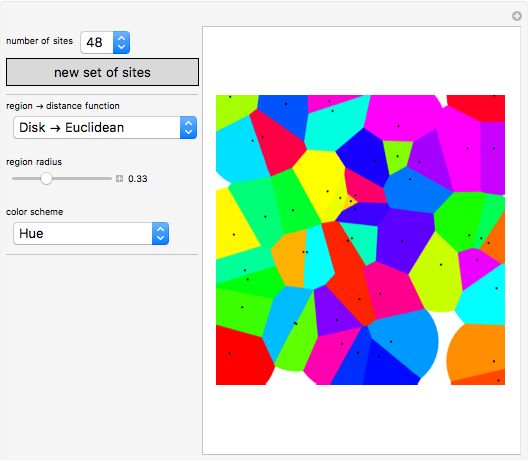
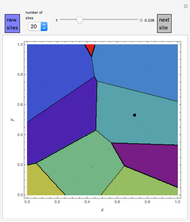
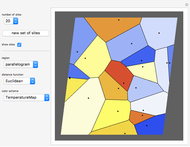
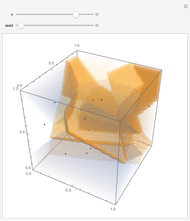
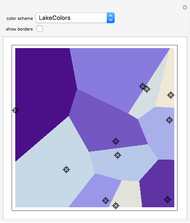
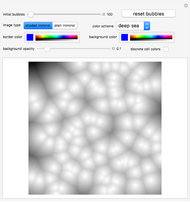
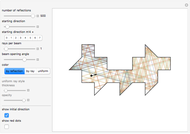
This Demonstration shows how a Voronoi diagram can be constructed from a set of expanding cells centered at a given number of sites. Depending on the distance function, the cell can be a disk or polygon.
[more]
Contributed by: Erik Mahieu (August 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Constructing Voronoi Diagrams with Expanding Cells"
http://demonstrations.wolfram.com/ConstructingVoronoiDiagramsWithExpandingCells/
Wolfram Demonstrations Project
Published: August 8 2016