Convexification

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
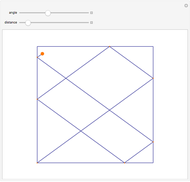
For a simply connected polygon  , convexification is the process of taking the convex hull
, convexification is the process of taking the convex hull  of
of  and then, for any side
and then, for any side  of
of  that is not part of
that is not part of  , reflecting the part of
, reflecting the part of  inside
inside  over the segment
over the segment  . Iterating the process eventually leads to a convex shape.
. Iterating the process eventually leads to a convex shape.
Contributed by: Robert Dickau, George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
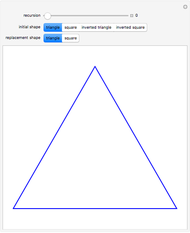
Snapshot 1: a regular star requires only one convexification to become a convex figure
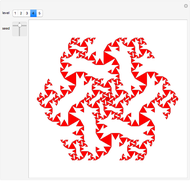
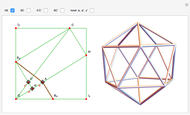
Snapshots 2, 3: the convexification of a figure often appears unlike the original figure
Reference: Z. A. Melzak, Invitation to Geometry, Mineola, NY: Dover, 2008.
Permanent Citation
"Convexification"
http://demonstrations.wolfram.com/Convexification/
Wolfram Demonstrations Project
Published: March 7 2011