Degenerate Eigenstates

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
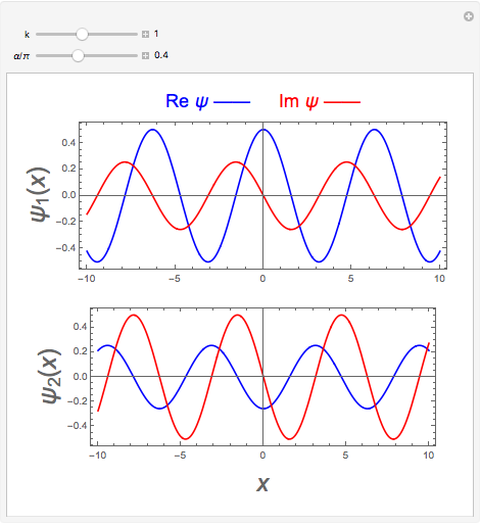
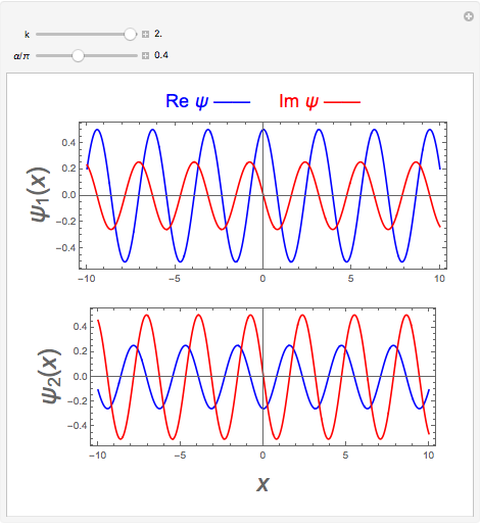
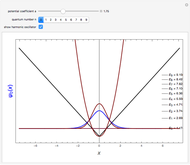
In quantum mechanics, if any eigenstate is  -fold degenerate, there are an infinite number of choices for the
-fold degenerate, there are an infinite number of choices for the  orthogonal eigenfunctions. The simplest possible example is the free particle in one dimension. Every energy level
orthogonal eigenfunctions. The simplest possible example is the free particle in one dimension. Every energy level  is twofold degenerate. This corresponds to the physical fact that particles moving in opposite directions have the same kinetic energy. The Schrödinger equation
is twofold degenerate. This corresponds to the physical fact that particles moving in opposite directions have the same kinetic energy. The Schrödinger equation  has two linearly independent eigenfunctions. A common choice takes
has two linearly independent eigenfunctions. A common choice takes  . These functions are delta function-normalized, such that
. These functions are delta function-normalized, such that  , and are also eigenfunctions of linear momentum
, and are also eigenfunctions of linear momentum  , with the eigenvalues
, with the eigenvalues  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
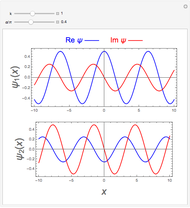
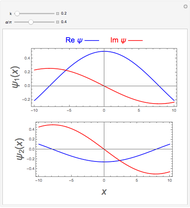
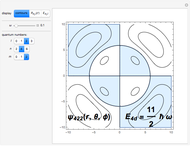
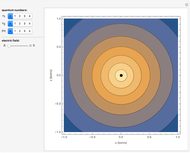
Snapshots 1 and 2: varying values of 
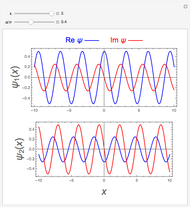
Snapshot 3: for  , the eigenfunctions are proportional to
, the eigenfunctions are proportional to  and
and 
Reference: S. M. Blinder, Introduction to Quantum Mechanics, Amsterdam: Elsevier, 2004 pp. 31–32.
Permanent Citation