Enveloping the Oloid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
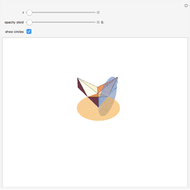
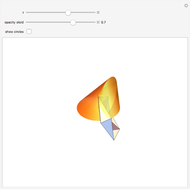
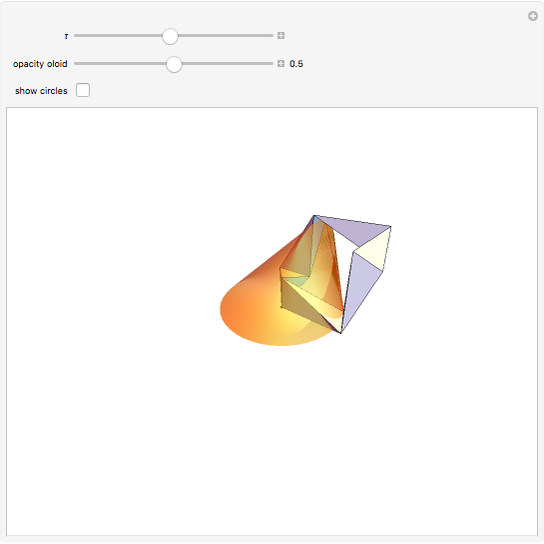
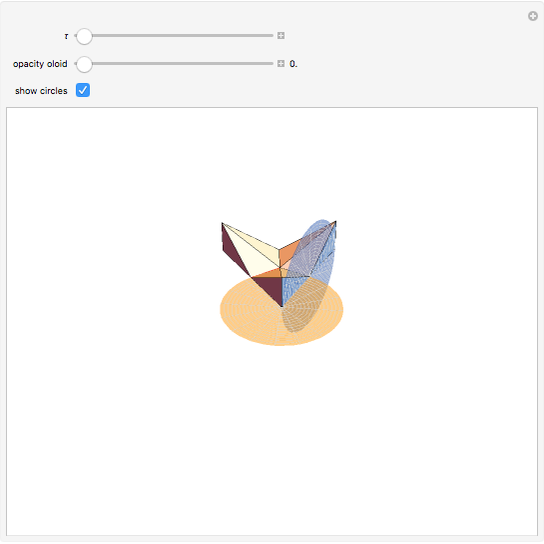
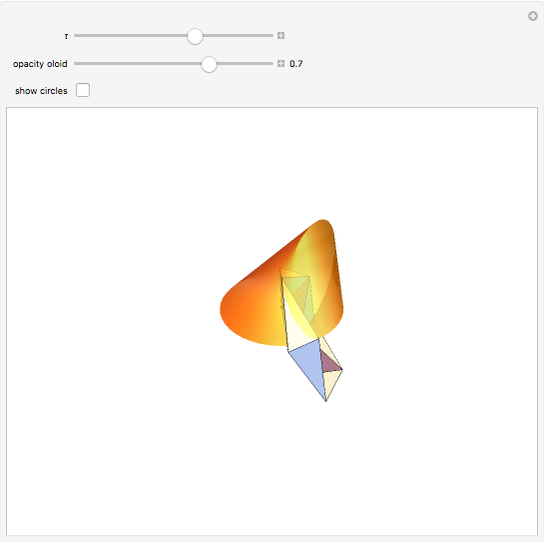
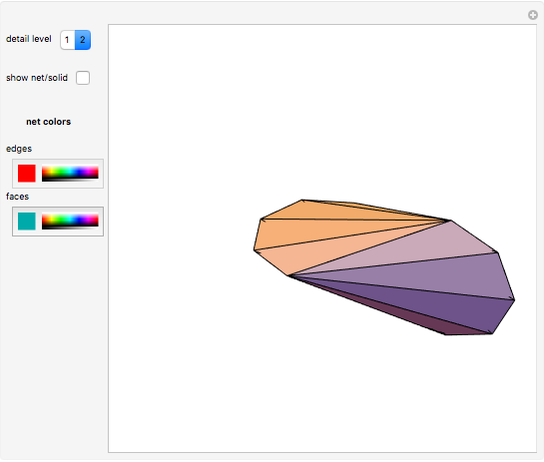
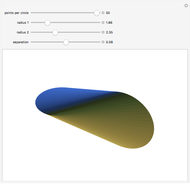
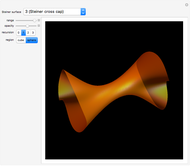
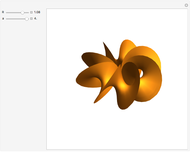
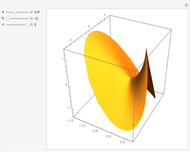
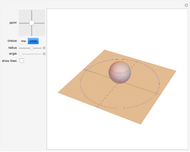
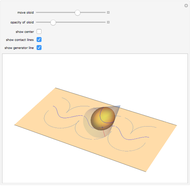
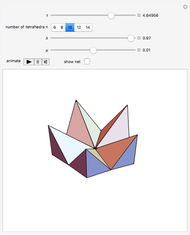
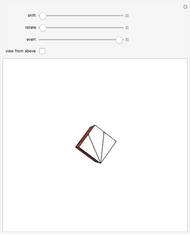
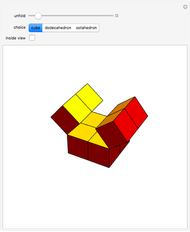
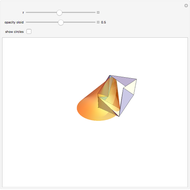
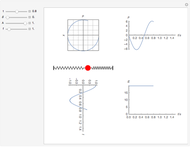
The oloid is the convex hull of two unit circles that lie in perpendicular planes where each circle contains the center of the other; you can show these circles. This Demonstration visualizes how the oloid develops from the inversion of a rectangular kaleidocycle, the center part of the evertible cube from Paul Schatz. The red line connects two vertices of the tetrahedra that form the kaleidocycle. This line is always tangent to the surface of the oloid, so when the line is moved by inverting the kaleidocycle it envelops the oloid. Some of the tetrahedra are hidden by the oloid; to make them visible, decrease the opacity of the oloid.
Contributed by: Hans-Joachim Domke (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
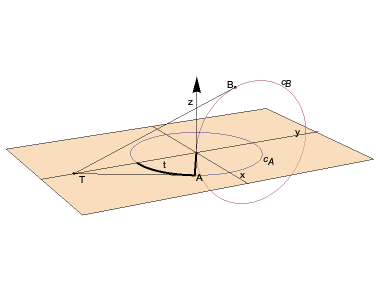
To describe the oloid parametrically, we calculate the coordinates of the two points  and
and  that are the endpoints of the red line. Let
that are the endpoints of the red line. Let 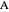 be a point on the circle
be a point on the circle 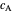 that lies in the
that lies in the 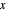 -
-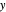 plane with center at the origin, so that
plane with center at the origin, so that 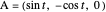 .
.
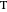 is the intersection of the tangent to
is the intersection of the tangent to 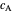 at
at 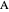 with the
with the 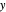 axis.
axis. 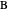 is the point that lies on the circle
is the point that lies on the circle 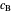 perpendicular to
perpendicular to 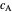 with center
with center 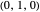 . The tangent to
. The tangent to 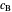 at
at 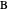 has the same intersection
has the same intersection 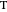 , so the points
, so the points  and
and 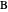 are coupled through their conjugate
are coupled through their conjugate  . With
. With 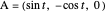 ,
, 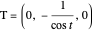 , and
, and 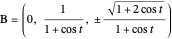 (the signs correspond to the upper and lower hemispheres). Interestingly, the length of
(the signs correspond to the upper and lower hemispheres). Interestingly, the length of 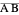 is always equal to
is always equal to  .
.
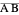 is also the set of points that touch the ground when the oloid lies on a plane, so when the plane is inclined, the contact points move over the surface of the oloid like the red line. This means that every point of the surface of the oloid touches with the plane as it moves forward. The movement is somewhat staggering but follows a straight line.
is also the set of points that touch the ground when the oloid lies on a plane, so when the plane is inclined, the contact points move over the surface of the oloid like the red line. This means that every point of the surface of the oloid touches with the plane as it moves forward. The movement is somewhat staggering but follows a straight line.
The parametric description of the oloid is 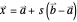 , with the parameters
, with the parameters 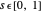 and
and 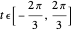 . The parameter
. The parameter  is restricted because we must have
is restricted because we must have 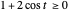 . Paul Schatz found the oloid in 1933 by imagining its shape while he studied the movement of the kaleidocycle. See http://www.paul-schatz.ch/.
. Paul Schatz found the oloid in 1933 by imagining its shape while he studied the movement of the kaleidocycle. See http://www.paul-schatz.ch/.
Reference
[1] H. Dirnböck and H. Stachel, "The Development of the Oloid," Journal for Geometry and Graphics, 1(2), 1997 pp. 105–118.
Permanent Citation