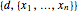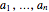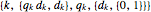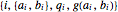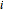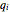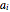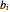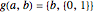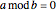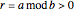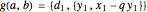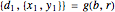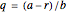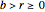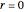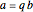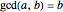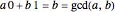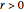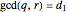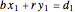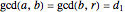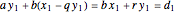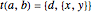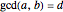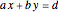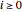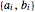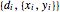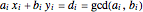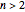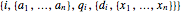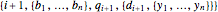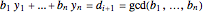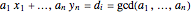Recursive Extended Euclidean Algorithm

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
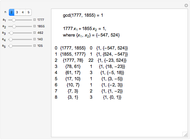
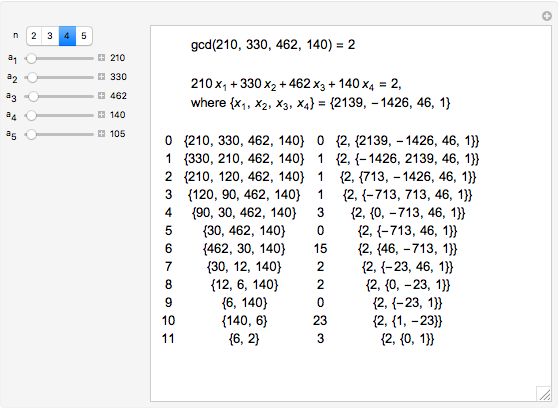
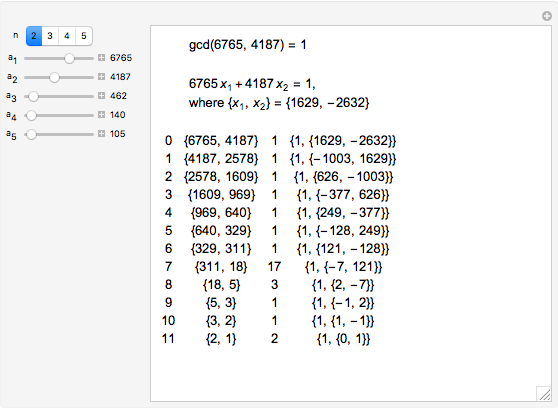
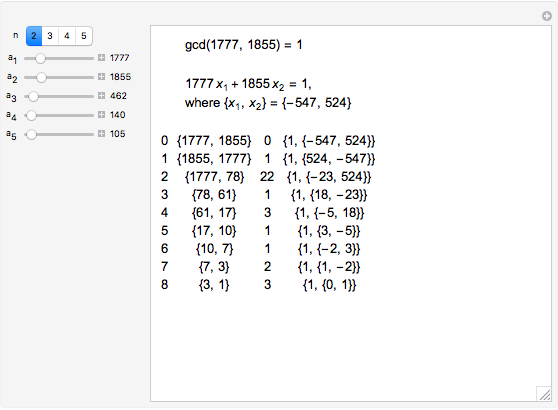
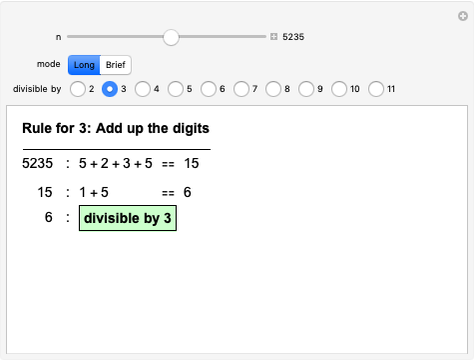
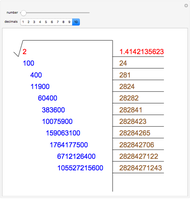
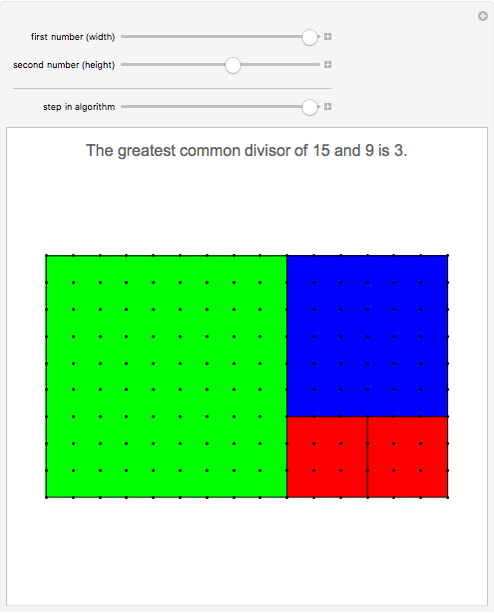
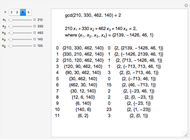
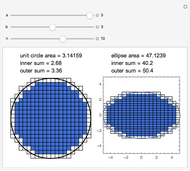
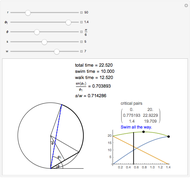
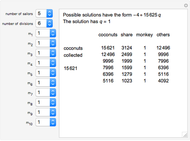
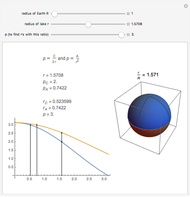
The greatest common divisor of positive integers 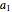 ,
, 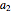 , …,
, …, 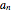 is the largest integer
is the largest integer  such that
such that  divides each of the
divides each of the  integers. There always exist integers
integers. There always exist integers 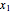 ,
, 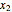 , …,
, …, 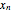 such that
such that 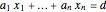 .
.
Contributed by: Roger B. Kirchner (March 2011)
Open content licensed under CC BY-NC-SA
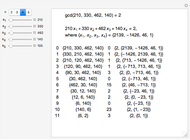
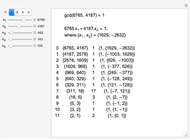
Snapshots
Details
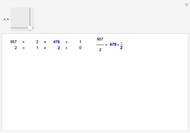
The correctness of the recursive definitions in the source code can be argued by observing 1) they terminate, 2) they return the correct result when they terminate, and 3) they return the correct result whenever a recursive call returns the correct result. The function in the program for  is
is 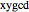 ; it is defined there for reference. Only
; it is defined there for reference. Only 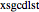 is used, however. It has a list of positive integers and a recursion level for inputs and returns the list that is displayed.
is used, however. It has a list of positive integers and a recursion level for inputs and returns the list that is displayed.
A classic exposition of these ideas is found in "1.7 The Euclidean Algorithm", in Birkhoff and MacLane, which can be read online.
The recursive algorithm we have used (for  ) is essentially described in Euclidean algorithm, under "Extended Euclidean Algorithm".
) is essentially described in Euclidean algorithm, under "Extended Euclidean Algorithm".
G. Birkhoff and S. MacLane, A Survey of Modern Algebra, 4th ed., New York: MacMillan Publishing Co., 1977.
K. H. Rosen, Elementary Number Theory and its Applications, 4th ed., Reading, MA: Addison–Wesley, 2000.
Permanent Citation