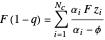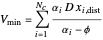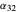Finding the Minimum Reflux Ratio Using the Underwood Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
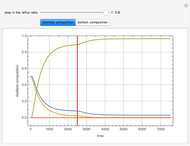
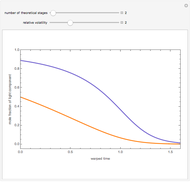
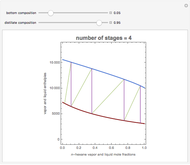
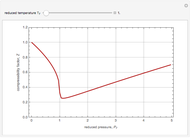
Consider a distillation column with a partial reboiler and a total condenser. This column is used to separate three hypothetical components 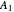 ,
, 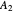 , and
, and 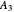 with relative volatilities
with relative volatilities 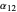 and
and  (i.e., the reference component is
(i.e., the reference component is 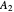 ) to be determined by the user. The calculation assumes that the reference component is the intermediate-boiling component,
) to be determined by the user. The calculation assumes that the reference component is the intermediate-boiling component, 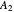 , and that the lightest and heaviest components are
, and that the lightest and heaviest components are  and
and 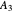 , respectively. The feed to the column has a thermal quality,
, respectively. The feed to the column has a thermal quality,  , also determined by the user. The feed composition is 40 mole%
, also determined by the user. The feed composition is 40 mole% 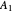 , 30 mole%
, 30 mole% 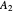 , and 30 mole%
, and 30 mole% 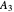 . The fractional recoveries in the distillate of components
. The fractional recoveries in the distillate of components 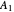 and
and 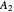 are 98% and 95%, respectively. The fractional recovery in the bottom of component
are 98% and 95%, respectively. The fractional recovery in the bottom of component 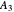 is 95%. The distillate rate,
is 95%. The distillate rate, 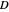 , can be computed from the equations
, can be computed from the equations  and
and 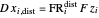 for
for 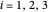 , where
, where  stands for fractional recovery. One can use as a basis a feed flow rate equal to 100 kmol/hr. In such a case, the distillate rate
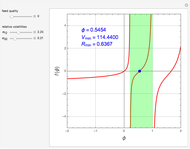
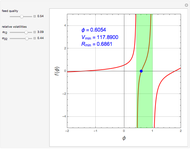
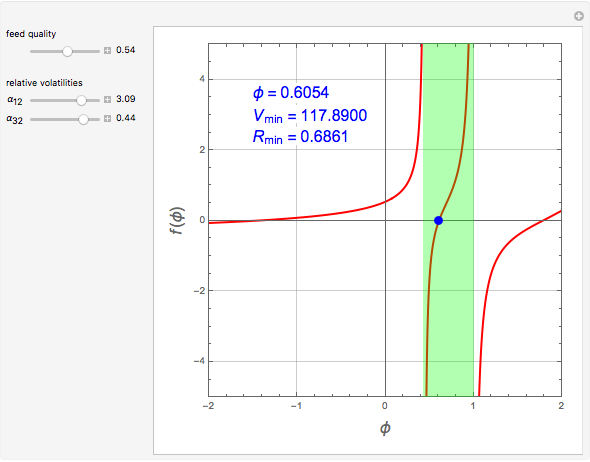
stands for fractional recovery. One can use as a basis a feed flow rate equal to 100 kmol/hr. In such a case, the distillate rate  kmol/hr. The Demonstration applies the Underwood equations [1] in order to determine the minimum reflux ratio,
kmol/hr. The Demonstration applies the Underwood equations [1] in order to determine the minimum reflux ratio, 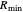 .
.
Contributed by: Housam Binous (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] P. C. Wankat, Separation Process Engineering, 2nd ed., Upper Saddle River, NJ: Prentice Hall, 2007.
Permanent Citation