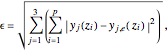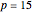Solving Stefan-Maxwell Equations Using Orthogonal Collocation and Shooting Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
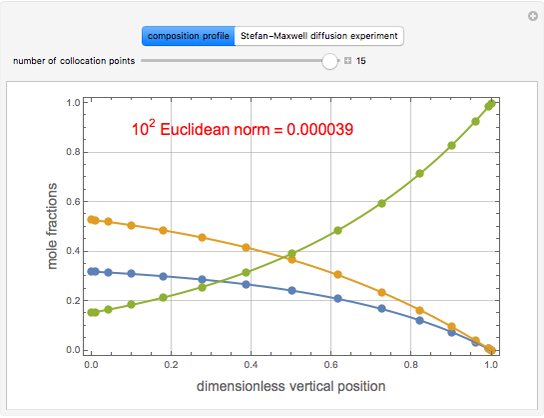
Consider acetone and methanol diffusing concurrently through a stagnant air column. The mole fractions of all three components are obtained by solving the species balance equation augmented with the Stefan–Maxwell equations for the diffusion fluxes. The resulting nonlinear boundary value problem can be solved using either a shooting method or by implementing an orthogonal collocation technique. In this Demonstration we use both methods. The plot shows the steady state concentration profiles of the three species in the diffusion column. The solid curves were obtained with a shooting technique using the terminal concentrations  ,
, 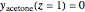 ,
, 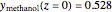 , and
, and 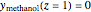 , using Mathematica's built-in function NDSolve. The blue, magenta, and brown colors correspond to acetone, methanol, and air, respectively. The colored dots shows the solution obtained using the orthogonal collocation technique for user-set values for the number of interior collocation points. As expected, excellent agreement is seen between both numerical methods.
, using Mathematica's built-in function NDSolve. The blue, magenta, and brown colors correspond to acetone, methanol, and air, respectively. The colored dots shows the solution obtained using the orthogonal collocation technique for user-set values for the number of interior collocation points. As expected, excellent agreement is seen between both numerical methods.
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (April 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Stefan–Maxwell relationships for unidirectional diffusion are given by:
 for
for  , where
, where  is the flux of species
is the flux of species 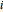 (expressed in
(expressed in 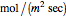 ). From the calculation we find that
). From the calculation we find that  and
and 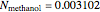 , while
, while 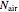 is assumed equal to zero. Binary diffusivities are equal to
is assumed equal to zero. Binary diffusivities are equal to  ,
,  , and
, and 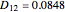 (all expressed in
(all expressed in 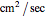 ).
).
References
[1] J. Benitez, Principles and Modern Applications of Mass Transfer Operations, New York: Wiley–Interscience, 2002.
[2] R. Carty and T. Schrodt, "Concentration Profiles in Ternary Gaseous Diffusion," Industrial Engineering and Chemistry Fundamentals, 14(3), 1975 pp. 276–278.
Permanent Citation