Integral Grid Triangles with Consecutive Side Lengths

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
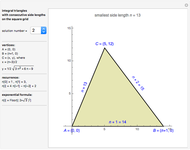
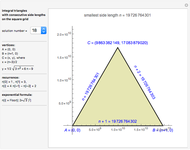
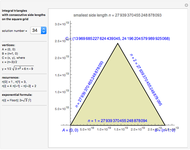
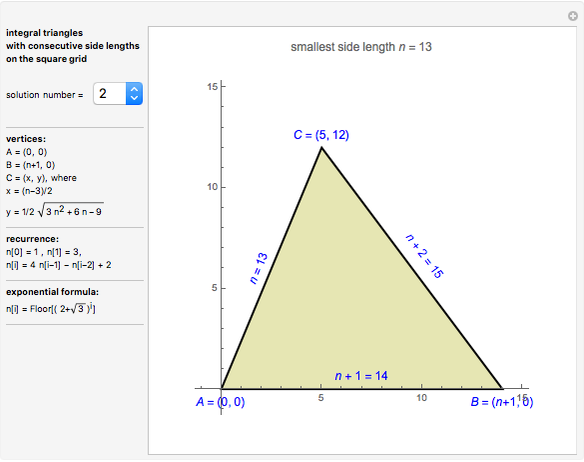
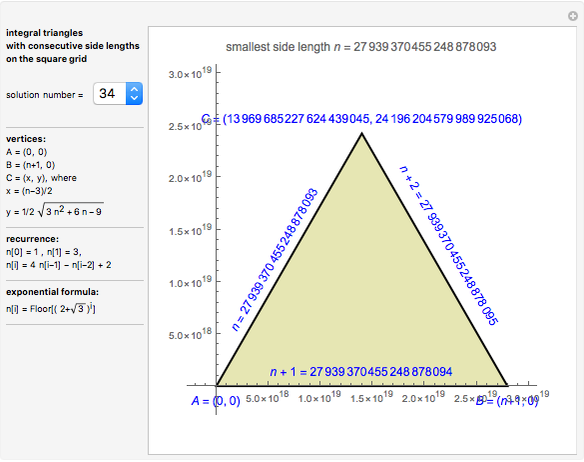
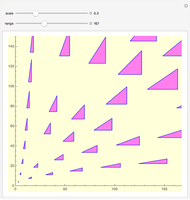
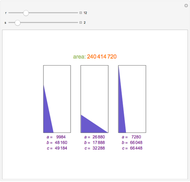
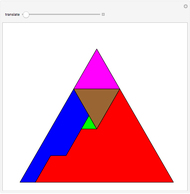
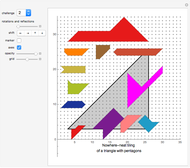
An integral triangle is a triangle with integral side lengths. This Demonstration shows those integral triangles that have consecutive numbers as side lengths and for which all three vertices have integral coordinates.
Contributed by: Karl Scherer (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Introduction
It can be shown that each consecutively integral triangle on the grid can be positioned such that
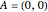 ,
, 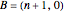 ,
, 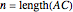 ,
,  , and
, and 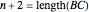 .
.
This Demonstration shows the first 50 solutions.
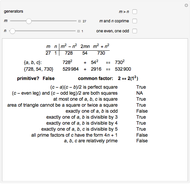
It also displays two ways to calculate the solutions: using a recurrence or using an exponential formula.
Generalization in 3D
In three or more dimensions the problem of finding all consecutive triangles is still unsolved.
Here are just three examples that have no equivalent in two dimensions:
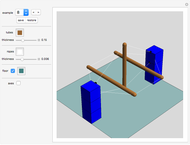
The triangle with vertices (0,0,0), (0,0,8), (6,3,2) has side lengths 7, 8, and 9.
The triangle with vertices (0,0,0), (0,0,10), (6,6,3) has side lengths 9, 10, and 11.
The triangle with vertices (0,0,0), (0,0,22), (18,6,9) has side lengths 21, 22, and 23.
Can you prove that these triangles do not fit on the two-dimensioinal integral lattice?
Can you find more examples?
In-depth discussion
The topic of consecutively integral triangles and also the more general topic of triangles on the grid with integral side lengths have been discussed in depth by the author in his book NUTTS And Other Crackers, 1994, privately published.
Many interesting recurrence relations are connected with this problem area.
Even the Lehmer–Lucas test for Mersenne prime numbers is related to these triangles!
Permanent Citation
"Integral Grid Triangles with Consecutive Side Lengths"
http://demonstrations.wolfram.com/IntegralGridTrianglesWithConsecutiveSideLengths/
Wolfram Demonstrations Project
Published: March 7 2011