Interleaving Theorems for the Rayleigh-Ritz Method in Quantum Mechanics

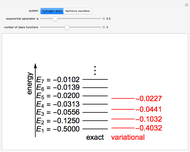
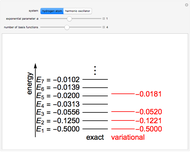
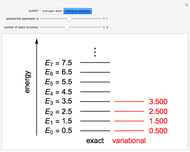
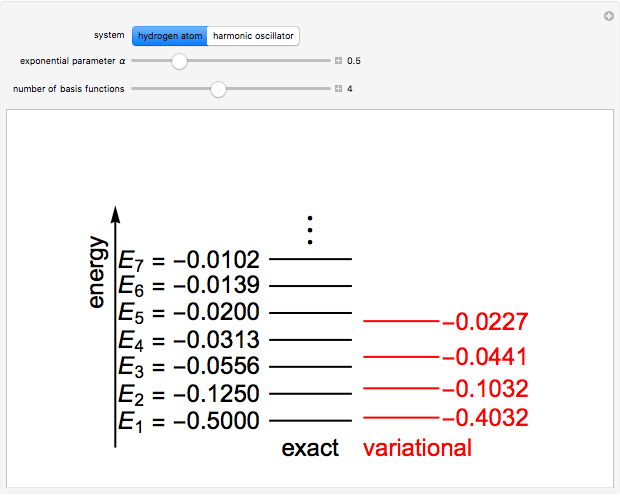
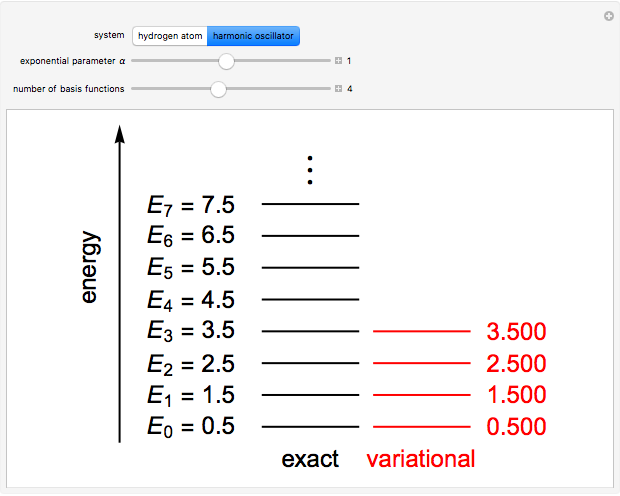
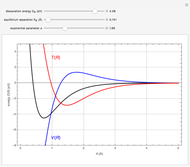
The Rayleigh–Ritz variational method has been well known in mathematics for well over a century. Its application to quantum mechanics was definitively described by J. K. L. MacDonald in Phys. Rev. 43(10), 1933 pp. 830–833. The eigenfunctions of a quantum-mechanical Hamiltonian can be approximated by a linear combination of basis functions. This gives an secular equation with roots, approximating the lowest eigenvalues. Two interleaving theorems can be proven: (1) between each pair of successive roots of the secular equation, augmented by and 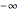, there occurs at least one exact eigenvalue; (2) if is increased to , then the new approximate roots will be interleaved by the previous ones. As a corollary to (1), often called simply "the" variational principle, the lowest approximate eigenvalue provides an upper bound to the exact ground-state eigenvalue.

In this Demonstration, the Rayleigh–Ritz method is applied to two simple quantum-mechanical problems—the hydrogen atom and the linear harmonic oscillator. For the hydrogen atom, the energy scale is distorted from the actual rapidly-converging spectrum. These are somewhat artificial problems in the sense that exact ground-state eigenvalues can be obtained with the exponential coefficients . But for , one can pretend that exact solutions are not available.