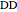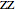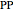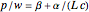Krugman's Model of Increasing Returns and Monopolistic Competition

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
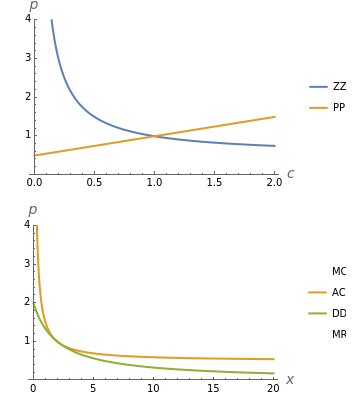
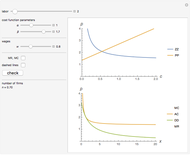
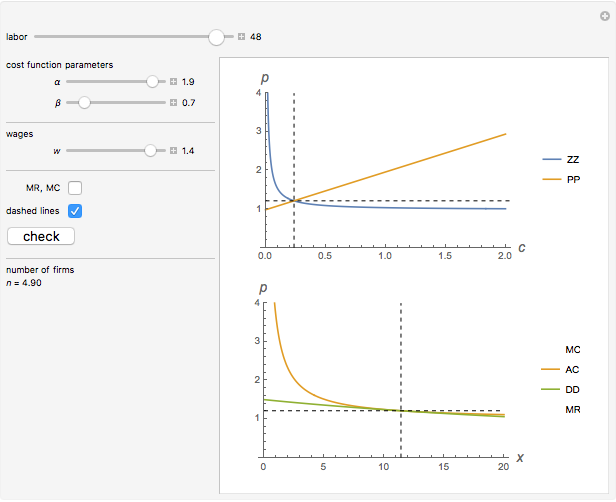
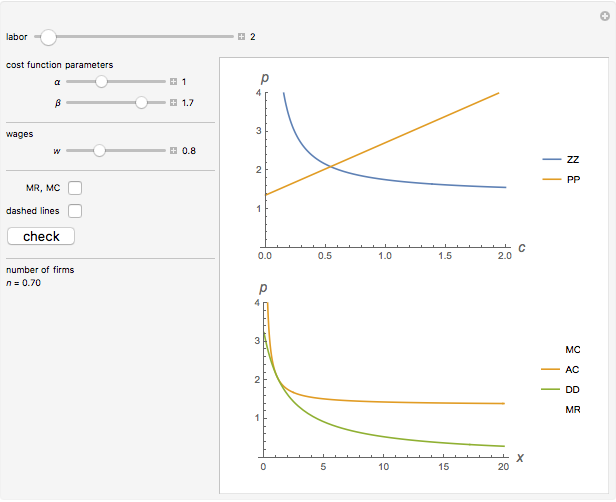
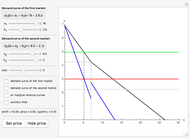
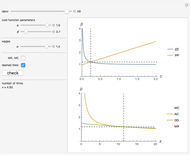
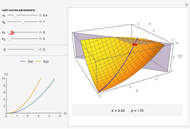
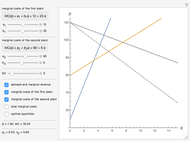
This Demonstration considers Krugman's model of increasing returns and monopolistic competition. Krugman's model can be applied to international trade or the economics of agglomerations. Originally, Krugman considered equilibrium in terms of the relationship between price 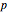 and consumption
and consumption  (upper plot). This Demonstration adds the more familiar inverse demand representation (bottom plot), which shows the relationship between price
(upper plot). This Demonstration adds the more familiar inverse demand representation (bottom plot), which shows the relationship between price 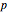 and the production quantity
and the production quantity  . Notice that the typical output of a firm and the typical consumption by an individual have the following dependence:
. Notice that the typical output of a firm and the typical consumption by an individual have the following dependence: 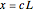 , where
, where  is the whole population (total labor)—that is, the main parameter of the model.
is the whole population (total labor)—that is, the main parameter of the model.
Contributed by: Timur Gareev (June 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
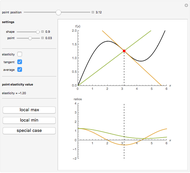
Krugman considered the inverse demand function in a general form 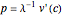 and that
and that 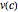 should be chosen such that elasticity of demand
should be chosen such that elasticity of demand  decreases with
decreases with  . The usual requirements
. The usual requirements  ,
, 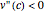 also apply. To visualize the model, we take
also apply. To visualize the model, we take  , which provides the most tractable results:
, which provides the most tractable results:
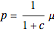 ,
,
where 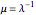 .
.
One may check that elasticity 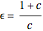 is decreasing with
is decreasing with  . Remember that
. Remember that 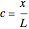 , where
, where  is an exogenous population.
is an exogenous population.
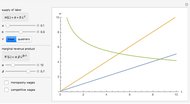
Increasing returns in the one-factor case 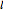 can be modeled as
can be modeled as 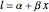 , which is the inverse production function.
, which is the inverse production function.
To get the total costs function, we need the factor price 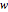 :
:
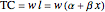 ,
,
so average costs are:
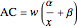 .
.
In the monopolistic competition case, the following system should be resolved:
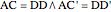 .
.
Interestingly, while solving the system we may simultaneously obtain
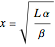
and
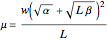 .
.
This solution shows how demand walks around the average costs curve while  changes (bottom plot). Notice that the number of firms in a growing market also increases, while individual consumption of each good decreases. This means growing diversity and volume of consumption for a representative consumer.
changes (bottom plot). Notice that the number of firms in a growing market also increases, while individual consumption of each good decreases. This means growing diversity and volume of consumption for a representative consumer.
Unlike Krugman's original paper, we put 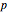 on the vertical axis of the upper plot instead of
on the vertical axis of the upper plot instead of 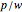 , but as
, but as 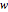 is exogenous, this does not influence the exposition (we just let the upper plots depend on the
is exogenous, this does not influence the exposition (we just let the upper plots depend on the 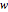 parameter).
parameter).
This model may describe international trade or agglomeration effects because an increase of  corresponds to market extension. This simple model ignores transportation costs, but they may be incorporated as well, as Krugman shows in his later works.
corresponds to market extension. This simple model ignores transportation costs, but they may be incorporated as well, as Krugman shows in his later works.
Reference
[1] P. R. Krugman, "Increasing Returns, Monopolistic Competition, and International Trade," Journal of International Economics, 9(4), 1979 pp. 469–479. doi:10.1016/0022-1996(79)90017-5.
Permanent Citation