Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Sierpinski 3D Arrowhead Curve

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

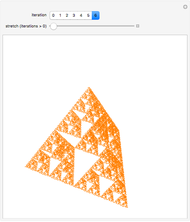
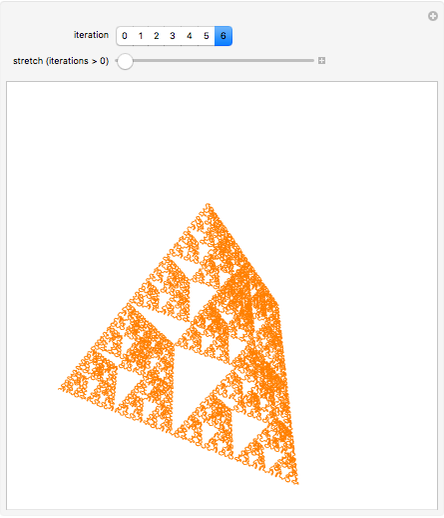
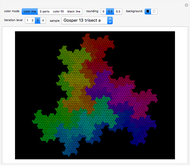
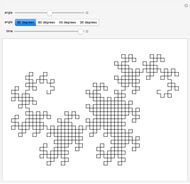
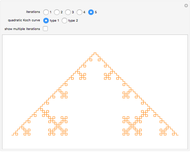
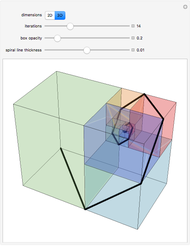
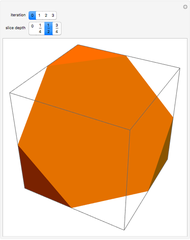
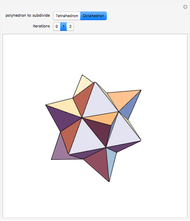
The Sierpinski arrowhead curve is a classic fractal that approximates the Sierpinski triangle. Like many two-dimensional fractal curves, it can be extended to three dimensions; this extension approximates the tetrix (or Sierpinski tetrahedron).

Contributed by: Robert Dickau (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

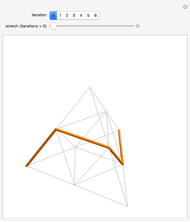
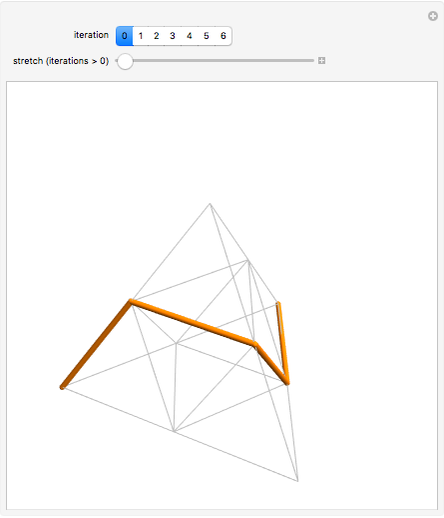
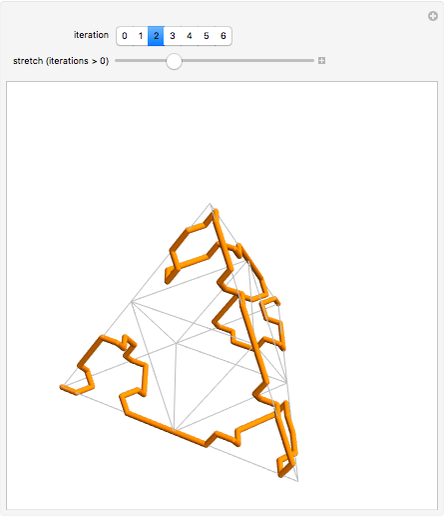
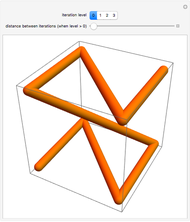
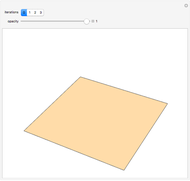
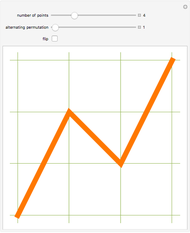
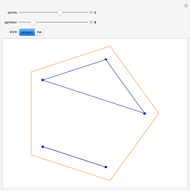
Snapshot 1: creation of the figure begins with a simple seed

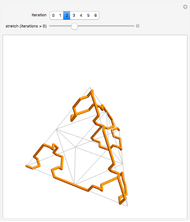
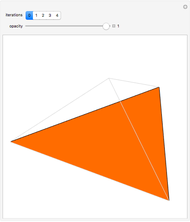
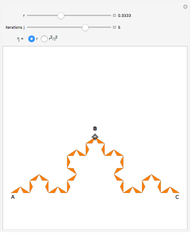
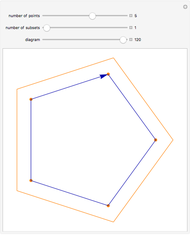
Snapshot 2: each iteration is created by rotating and translating the previous image in such a way that the endpoints match up, making an unbroken curve; increasing the "stretch" factor between iterations emphasizes how the figure is connected

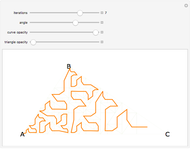
Snapshot 3: higher iterations approximate the tetrix

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send