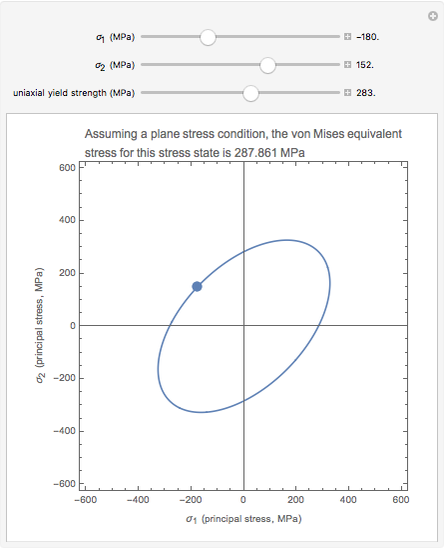
Metallicity Condition and Electronic Density of States in Achiral Single-Walled Carbon Nanotubes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
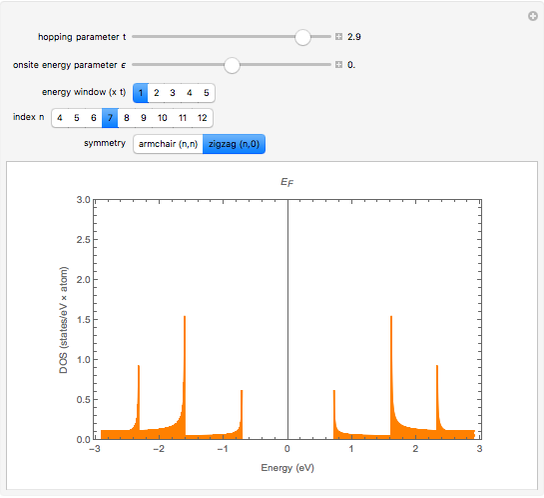
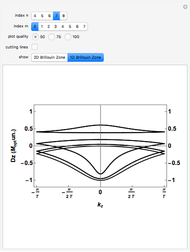
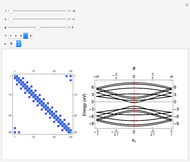
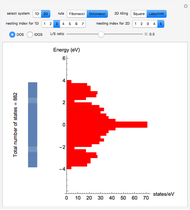
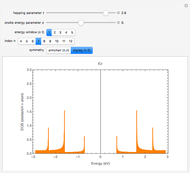
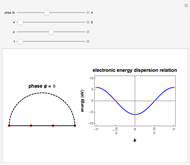
This Demonstration plots the electronic density of states (DOS) computed from the tight-binding method for zigzag ( ) and armchair (
) and armchair ( ) single-walled carbon nanotubes (SWNTs). The spikes in the electronic DOS profile are called van Hove singularities (vHs) and originate from the different values of the azimuthal band quantum number
) single-walled carbon nanotubes (SWNTs). The spikes in the electronic DOS profile are called van Hove singularities (vHs) and originate from the different values of the azimuthal band quantum number  . The total number of allowed
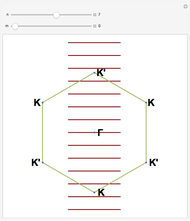
. The total number of allowed  values is determined by the number of graphene unit cells inside the SWNT cell, which is always
values is determined by the number of graphene unit cells inside the SWNT cell, which is always  for achiral SWNTs. By playing with the chiral pairs
for achiral SWNTs. By playing with the chiral pairs  , you can verify the metallicity condition for these achiral SWNTs:
, you can verify the metallicity condition for these achiral SWNTs: 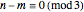 for metallic SWNTs and
for metallic SWNTs and  for semiconducting SWNTs. For metallic SWNTs the electronic DOS is nonzero at the Fermi level, whereas for semiconducting SWNTs, a gap occurs at the Fermi level. Armchair SWNTs are always metallic for any
for semiconducting SWNTs. For metallic SWNTs the electronic DOS is nonzero at the Fermi level, whereas for semiconducting SWNTs, a gap occurs at the Fermi level. Armchair SWNTs are always metallic for any  . By changing the sliders related to the tight-binding parameters
. By changing the sliders related to the tight-binding parameters  and
and  you can change the value of the energy at which the vHs occur and the asymmetry of the electronic structure with respect to the Fermi level (
you can change the value of the energy at which the vHs occur and the asymmetry of the electronic structure with respect to the Fermi level ( ).
).
Contributed by: Jessica Alfonsi (University of Padova, Italy) (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
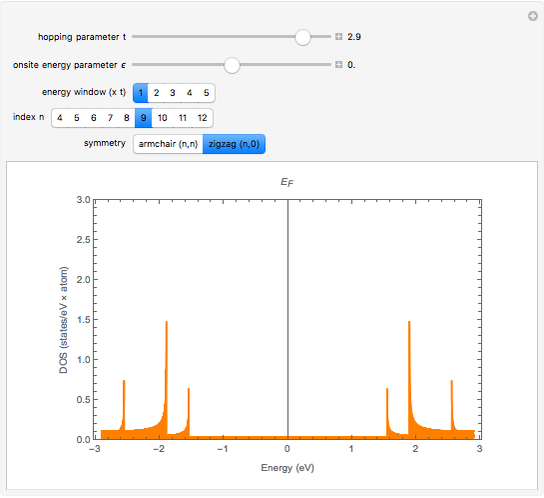
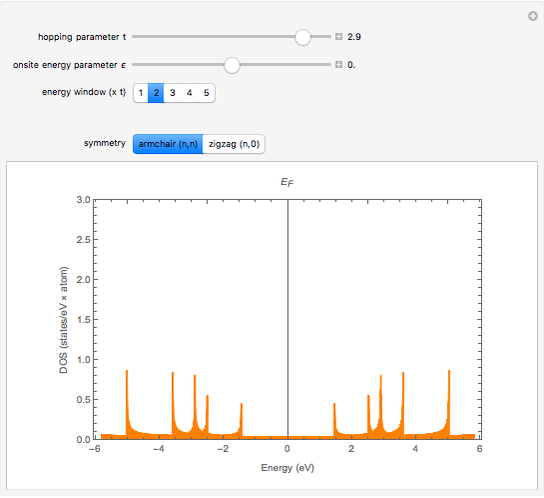
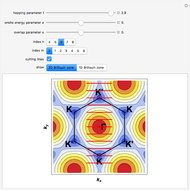
Electronic density of states:
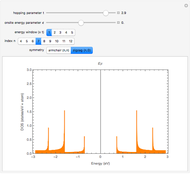
Snapshot 1: for a semiconducting zigzag (7,0) SWNT: 
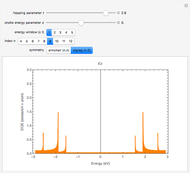
Snapshot 2: for a metallic zigzag (9,0) SWNT: 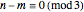
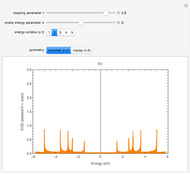
Snapshot 3: for an armchair (6,6) SWNT, always metallic: 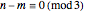
The analytical expressions used in the program were taken from [1].
Reference
[1] A. T. Costa, Jr., D. F. Kirwan, and M. S. Ferreira, "Indirect Exchange Coupling between Magnetic Adatoms in Carbon Nanotubes," Physical Review B 72(8), 2005. doi:10.1103/PhysRevB.72.085402.
Permanent Citation