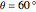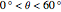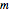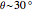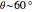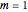Moiré Patterns and Commensurability in Rotated Graphene Bilayers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
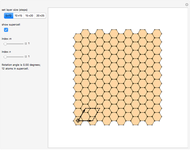
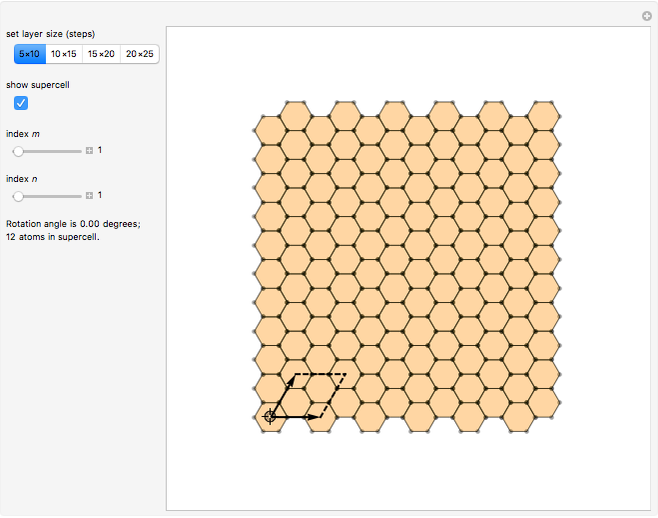
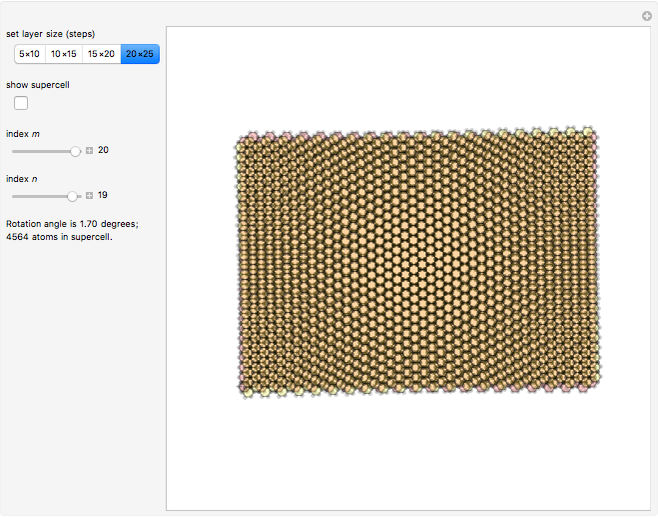
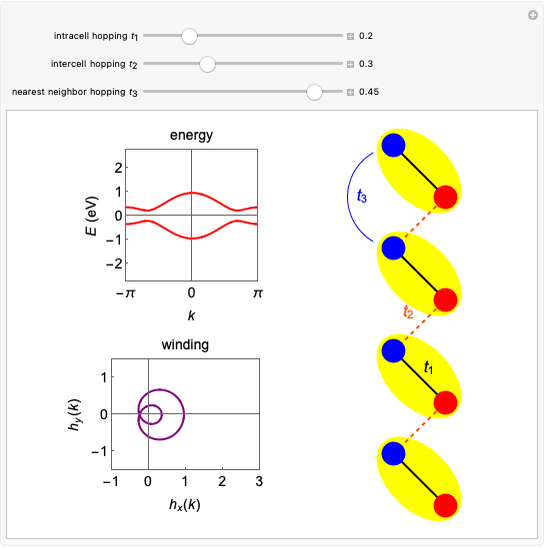
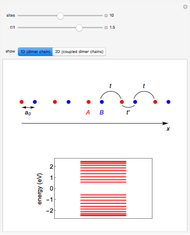
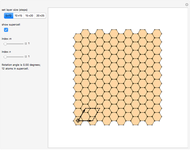
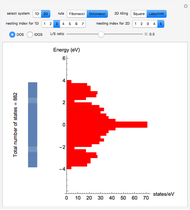
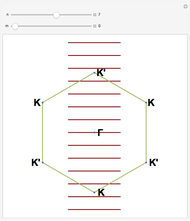
This Demonstration shows the appearance of Moiré patterns in hexagonal lattice systems as you rotate a honeycomb layer on top of another identical layer by an angle  . The rotation angle
. The rotation angle  can be freely chosen or, as done in this Demonstration, specified by a couple of integer indices
can be freely chosen or, as done in this Demonstration, specified by a couple of integer indices 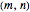 following [1]. These integers also give the number of atoms and the unit cell basis vectors of the supercell of the bilayer system. Some example systems where Moiré patterns on hexagonal lattices that have been recently experimentally observed are bilayer graphene systems.
following [1]. These integers also give the number of atoms and the unit cell basis vectors of the supercell of the bilayer system. Some example systems where Moiré patterns on hexagonal lattices that have been recently experimentally observed are bilayer graphene systems.
Contributed by: Jessica Alfonsi (December 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
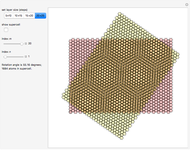
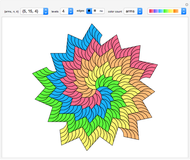
Snapshot 1: perfect AA stacking (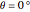 ) with
) with 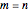
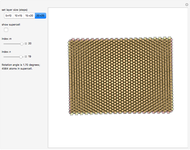
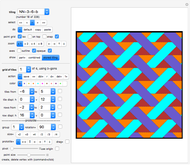
Snapshot 2: quasi-perfect AB stacking limit (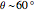 ) with large
) with large 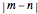
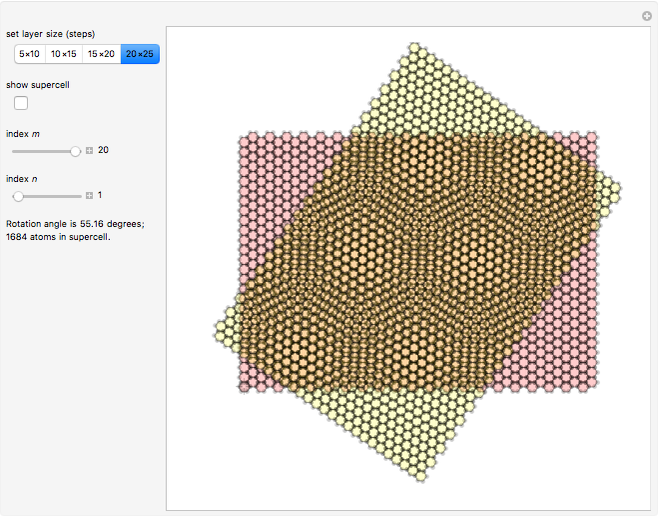
Snapshot 3: example of an extremely large supercell (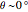 limit) with small
limit) with small 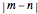
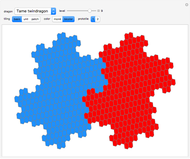
Snapshot 4: example of a commensurate bilayer cell 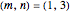 , symmetric with respect to the case in the thumbnail snapshot with
, symmetric with respect to the case in the thumbnail snapshot with 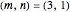
Reference
[1] G. T. de Laissardière, D. Mayou, and L. Magaud, "Localization of Dirac Electrons in Rotated Graphene Bilayers," Nano Letters, 10(3), 2010 pp. 804–808. pubs.acs.org/doi/abs/10.1021/nl902948m.
Permanent Citation