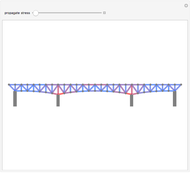
Method of Joints to Solve a Truss Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
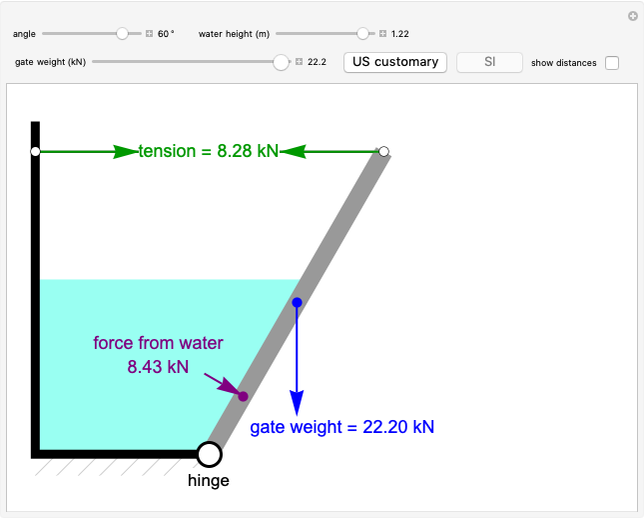
This Demonstration solves a truss using the method of joints, which involves doing force balances around one joint at a time.
[more]
Contributed by: Rachael L. Baumann (September 2017)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
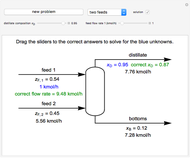
Snapshots
Details
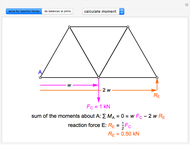
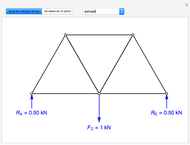
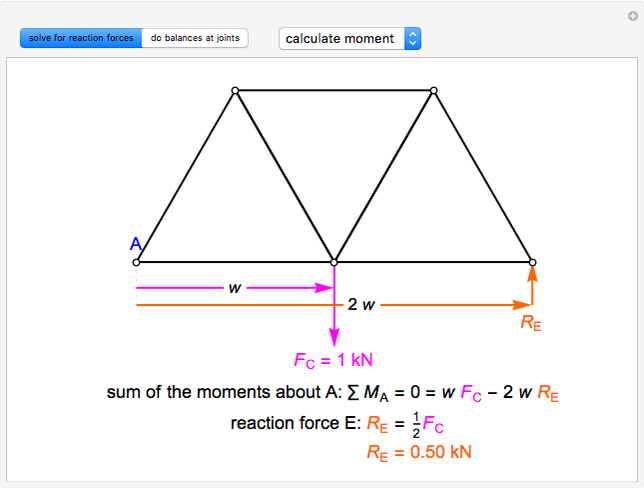
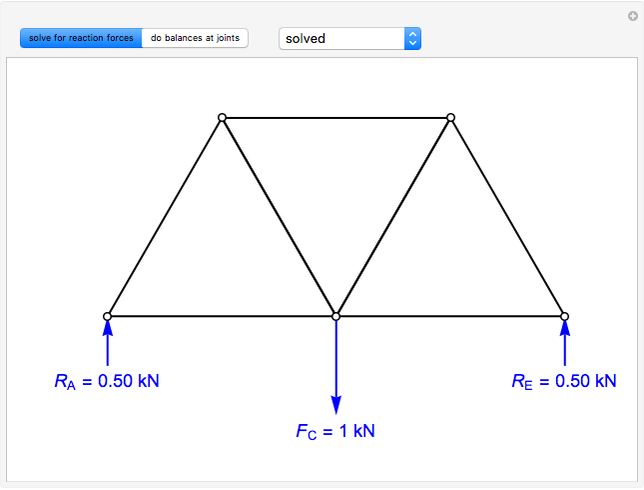
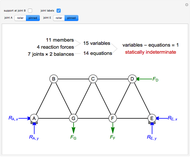
First, calculate the reaction forces by doing a moment balance around joint  and force balances in the
and force balances in the  and
and 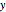 directions:
directions:
 ,
,
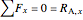 ,
,
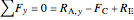 ,
,
where 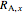 and
and  are the reaction forces at joint
are the reaction forces at joint  in the
in the  and
and 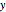 directions,
directions, 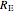 is the reaction force at joint
is the reaction force at joint  ,
,  is the width of the members and
is the width of the members and  is the point load force at joint
is the point load force at joint  .
.
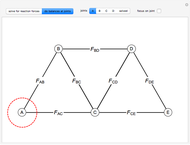
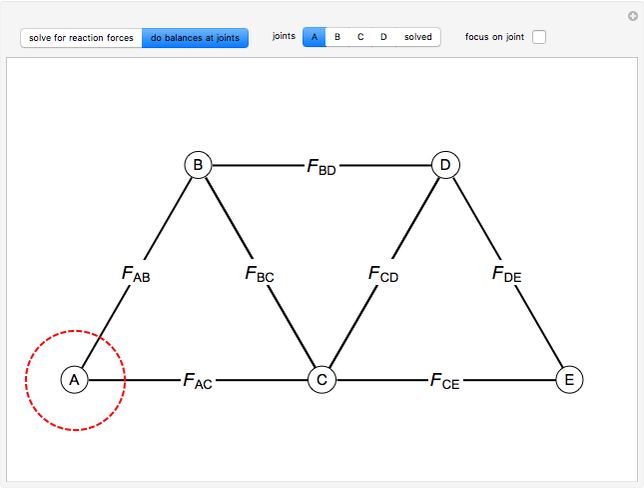
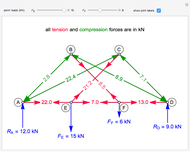
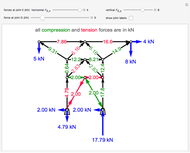
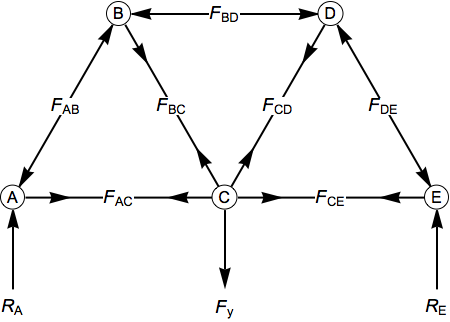
Next, do force balances at the joints. The order of the calculations shown is the order that the joints are solved in. Calculations are done assuming we know which members are under tension and which are under compression. View the labeled truss in Figure 1 below.
 ,
,
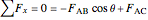 .
.
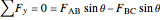 ,
,
 .
.
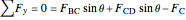 ,
,
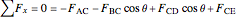 .
.
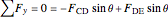 .
.
Figure 1
References
[1] R. C. Hibbeler, Engineering Mechanics: Statics, 12th ed., Upper Saddle River, NJ: Prentice Hall, 2010.
[2] D. Morrell. Truss Example-Method of Joints (Edited) [Video]. (Jun 6, 2012) www.youtube.com/watch?v=56eTM36Z9-A.
Permanent Citation