Newton's Rotating Bucket Experiment

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
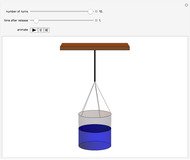
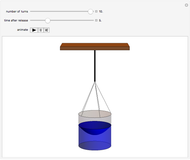
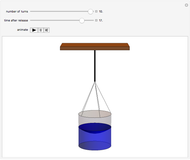
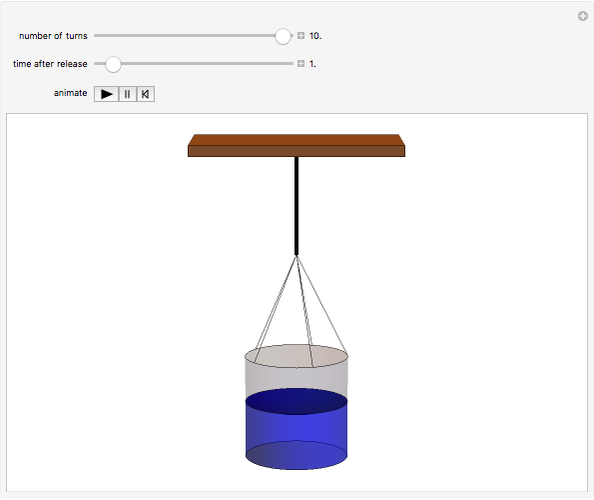
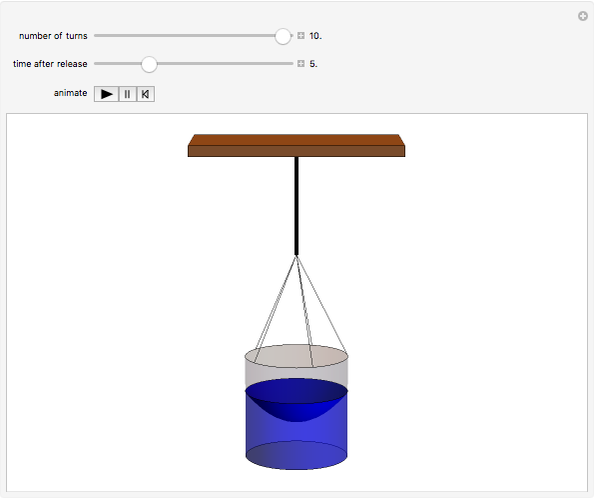
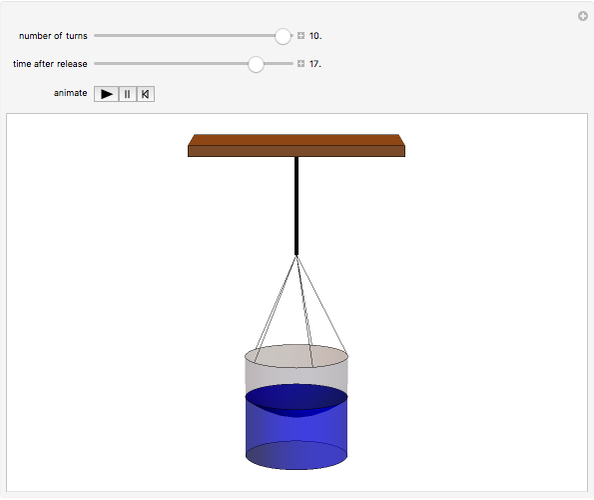
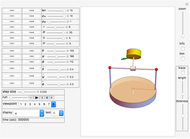
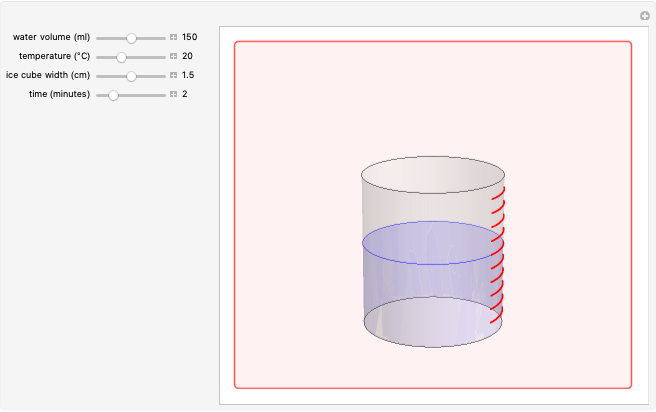
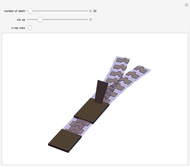
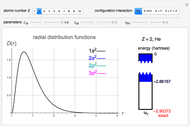
In the Scholium to Book 1 of Principia, Isaac Newton describes an experiment in which a bucket of water hung by a long cord is twisted and released. Initially, only the bucket rotates while the water remains stationary, as indicated by its flat surface. Gradually, the rotational motion is communicated to the water and centrifugal force distorts its surface into a paraboloid. After the bucket stops turning, the water continues to rotate until frictional forces again bring it to rest, flattening the paraboloid. (Viscosity, which causes this friction, is described by another law proposed by Newton!) Newton cited the rotating-bucket experiment to support his notion of absolute space as the reference frame for all motion. His contemporary Leibniz challenged Newton's worldview, arguing that space is actually created by the existence of material bodies. This debate continued into the twentieth century, principally associated with the writings of Mach and Einstein, and providing a philosophical underpinning for the general theory of relativity (see reference in Details).
[more]
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: as the bucket begins to rotate, the water remains stationary
Snapshot 2: the rotational motion is eventually communicated to the water, shown by its paraboloidal surface
Snapshot 3: after the bucket stops, the water continues to rotate until damped out by frictional forces
See the discussion in "The Universe and the Bucket," Chap. 2 in B. Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality, New York: Knopf, 2004.
Permanent Citation
"Newton's Rotating Bucket Experiment"
http://demonstrations.wolfram.com/NewtonsRotatingBucketExperiment/
Wolfram Demonstrations Project
Published: March 7 2011