Wolfram Demonstrations Project

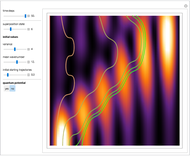
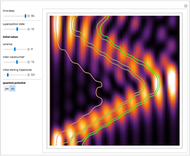
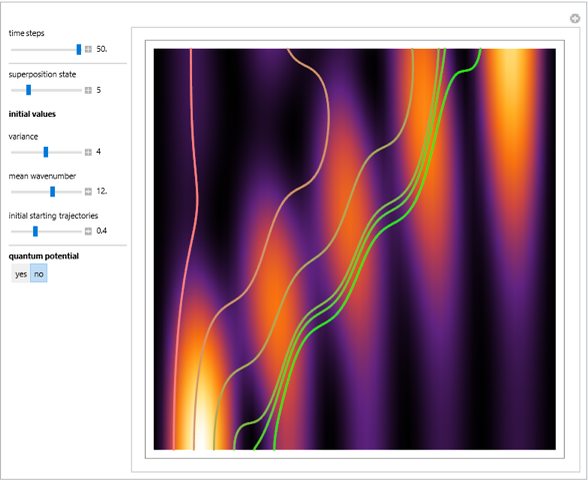
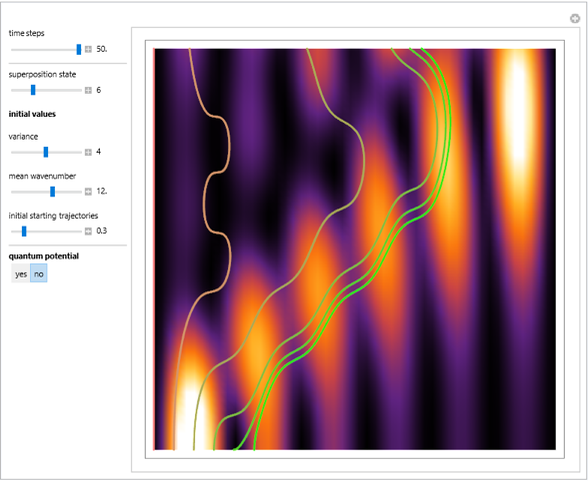
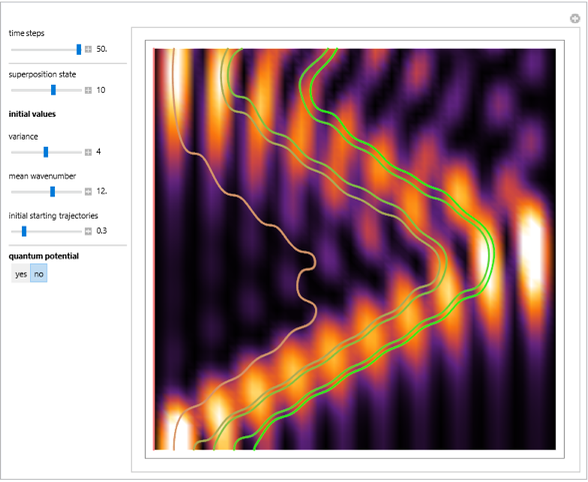
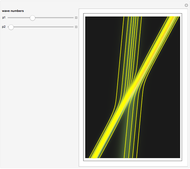
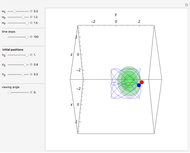
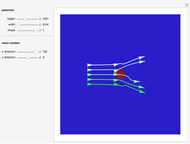
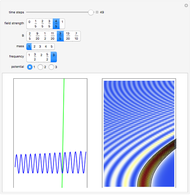
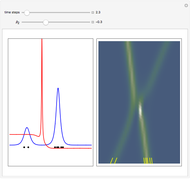
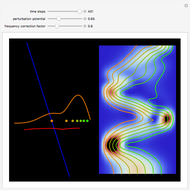
The principle of quantum superposition states that the complex-valued wavefunction can be a linear combination of several quantum eigenstates simultaneously. The modulus (or absolute value) squared of the total wave function represents a probability density of finding a quantum particle only. In the causal interpretation of quantum theory, developed in 1952 by David Bohm, the concept of trajectories is introduced, in which the particles are guided by a real phase function (or quantum potential) from the total wavefunction (pilot wave). In the eikonal representation, the phase function for a superposed state from which the velocity is determined becomes very complicated. This Demonstration discusses a superposition of up to 15 states of the density distribution for a quantum particle in the box with infinitely high walls. As the superposed wave packet spreads in an infinite square well, the paths of the quantum particles approach in a way similar to a classical trajectory.

The graphic shows the squared wavefunction, the possible trajectories of six quantum particles, and the contour plot of the quantum potential. Light areas correspond to large probability density whereas dark areas represent a low probability of finding a particle.

Contributed by: Klaus von Bloh
After work by: Enrique Zeleny

Slider Zoom
Gamepad Controls
Automatic Animation

The guiding equation for the particle velocity is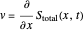

, which is calculated from the gradient of the phase of the wavefunction in the energy representation. In the eikonal form

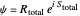the total wavefunction becomes

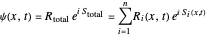In this case, the amplitude and the phase reduce to

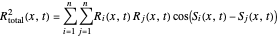
and

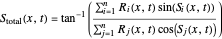from which the velocity is derived by differentiating the total phase function

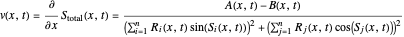
with

and

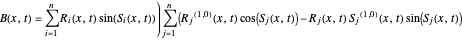where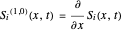

, and so on.

In the case that the phase function does not depend on the variable

, the velocity becomes

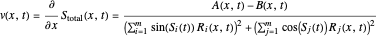
with

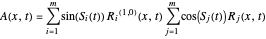
and

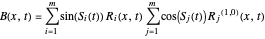which could be simplified to

Local singularities in the velocity

do appear to exist for certain

and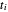

values (

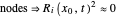), which makes the trajectories very unstable.

In the program, to make the results more accurate, increase PlotPoints, AccuracyGoal, PrecisionGoal, and MaxSteps.

References

[1] P. Holland, The Quantum Theory of Motion, Cambridge: Cambridge University Press, 1993.

[2] D. Bohm, Quantum Theory, New York: Prentice-Hall, 1951.

[3] I. Marzoli, F. Saif, I. Bialynicki-Birula, O. M. Friesch, A. E. Kaplan, and W. P. Schleich, "Quantum Carpets Made Simple." arXiv:quant-ph/9806033.