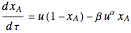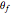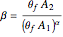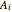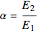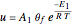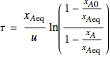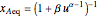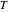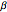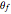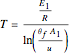Optimal Temperature Policy for First-Order Reversible Reactions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
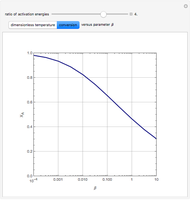
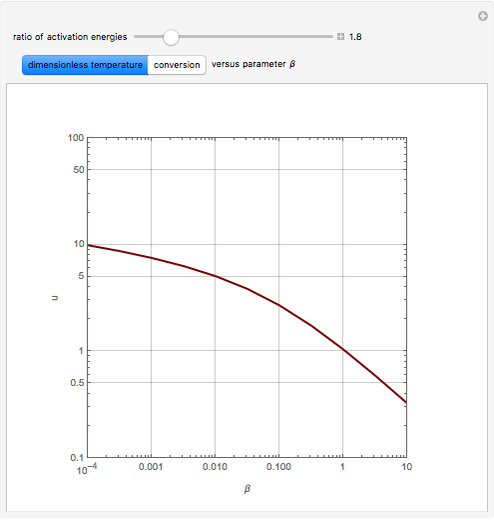
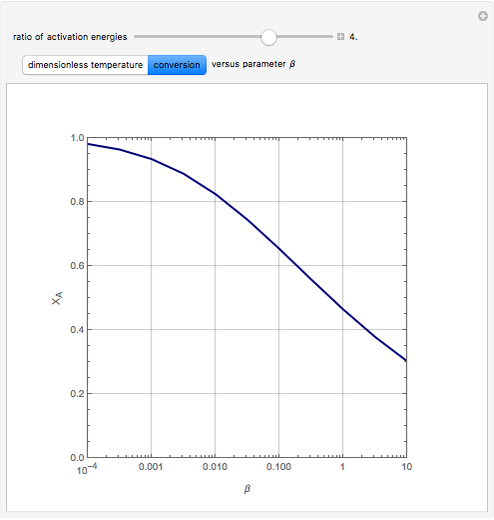
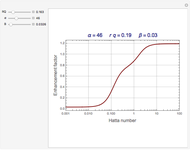
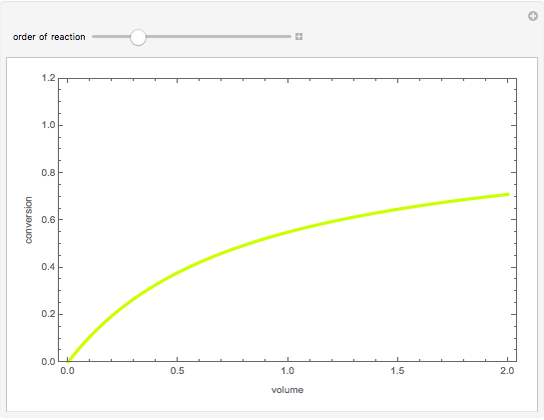
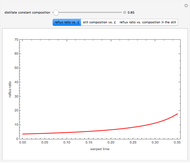
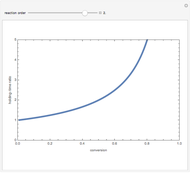
Consider the first-order reversible reaction involving chemical species 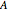 and
and 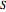 :
: 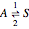 .
The reaction rate for
.
The reaction rate for 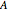 is given by:
is given by: 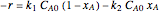 , where
, where 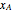 is the fraction of
is the fraction of 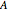 converted,
converted, 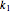 and
and  are the reaction rate constants, and
are the reaction rate constants, and 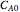 and
and 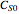 are the initial concentrations of species
are the initial concentrations of species 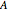 and
and 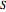 with
with 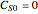 .
.
Contributed by: Housam Binous and Ahmed Bellagi (March 2011)
Open content licensed under CC BY-NC-SA
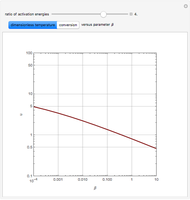
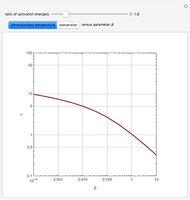
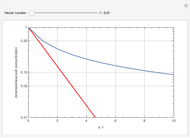
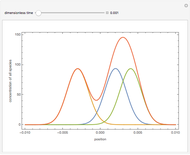
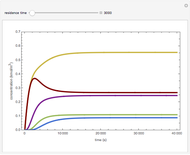
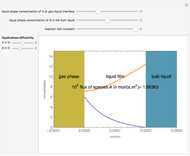
Snapshots
Details
C. D. Fournier and F. R. Groves, "Rapid Method for Calculating Reactor Temperature Profiles," Chem. Eng., 77(3), 1970 p. 121.
Permanent Citation