Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

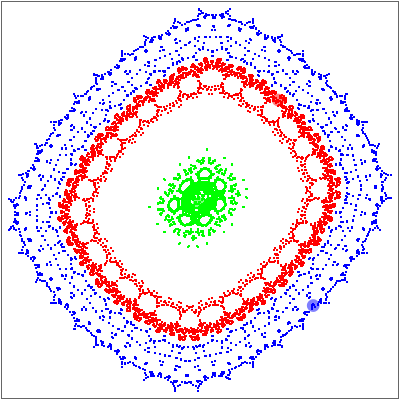
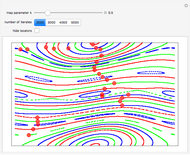
Orbits of Martin's Map

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

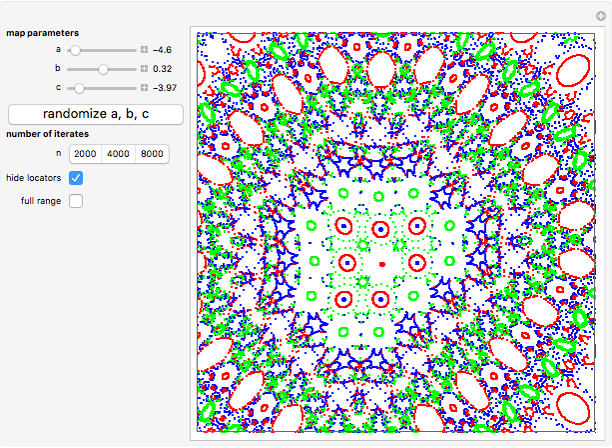
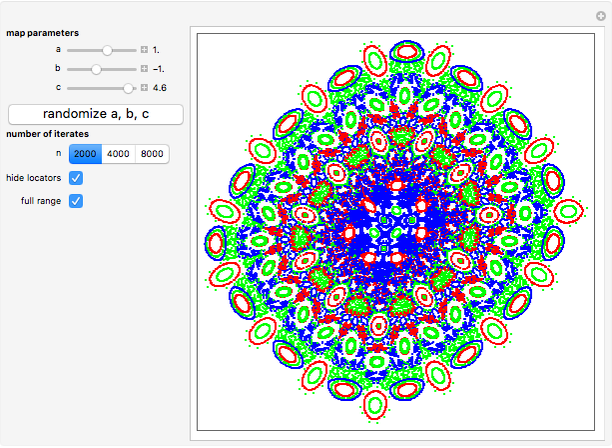
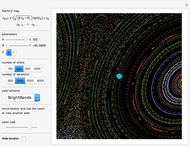
Orbits are generated by iterating the map times using different initial points. The map parameters , , and can be varied manually or a random set can be launched. Three orbits are plotted initially, starting from three different initial points marked by locator objects "". You can drag these initial points or add and/or delete new ones (Alt+Click on Windows) inside the plot. Three orbit colors are used cyclically.

Contributed by: Erik Mahieu (September 2009)
Open content licensed under CC BY-NC-SA

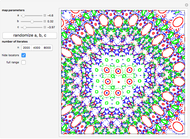
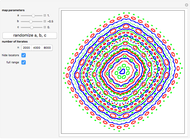
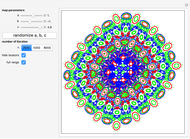
Snapshots

Details

All locator objects can be hidden for a "cleaner" plot. The plot range can be changed to full to include all points from all orbits.

The Martin map equations were taken from:

M. Trott, The Mathematica GuideBook for Programming, New York: Springer‐Verlag, 2004 pp. 347–349.

B. Martin, "Graphic Potential of Recursive Functions,"J. Landsdown, R. A. Earnshaw, eds., Computers in Art, Design and Animation, New York: Springer–Verlag, 1989 pp. 109–129.

The Martin Map is also called the "Hopalong-Attractor".

See also: Hopalong Image Generator and a German website: Huepfer.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send