Possible Calculation of Logarithms of Cosines in Vlacq's Trigonometria Artificialis

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
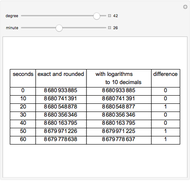
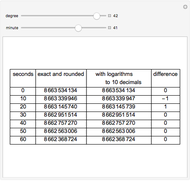
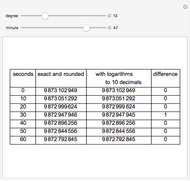
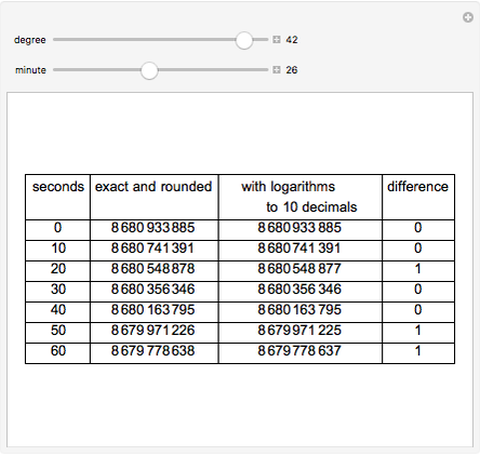
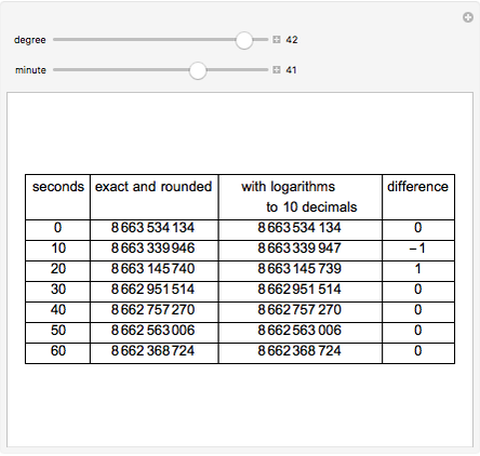
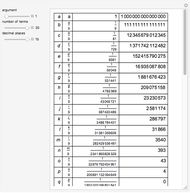
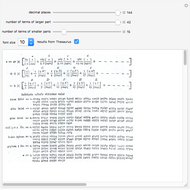
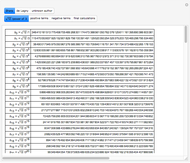
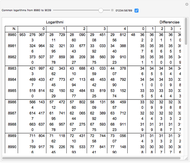
This Demonstration shows that the logarithms of cosines can be calculated using tables of trigonometric functions calculated to 15 decimals (such as the tables of Pitiscus) and tables of logarithms calculated to 10 decimals (such as Vlacq's 1628 tables) with aid of linear interpolation. Eventual errors are only one unit in the last decimal. In the grid, only the fractional part of 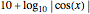 is given.
is given.
Contributed by: Izidor Hafner (April 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Errors that Gauss found in the trigonometric part of Vega's Thesaurus were actually from Vlacq's Trigonometria Artificialis.
According to [3, p. 5], Vlacq (1633) first computed the logarithms of the cosines from 0 to 45 degrees. This was done using the sines given by Rheticus in the Opus Palatinum (1596) where they are tabulated to 10 decimal places every 10 seconds, the same step as the one used by Vlacq. There are 16,200 logarithms and they could have been computed using Briggs' radix method.
According to [2, p.16], Vlacq's tables from 1628 were based on Pitiscus' Thesaurus Mathematicus, computing logarithms of known sines using the radix method.
References
[1] C. F. Gauss, "Einige Bemerkungen zu Vega's Thesaurus Logarithmorum," Astronomische Nachrichten, 32(756), 1851 pp. 181–188.
[2] D. Roegel. "A Reconstruction of De Decker-Vlacq's Tables in the Arithmetica Logarithmica (1628)." (Dec 6, 2010) hal.inria.fr/docs/00/54/39/41/PDF/vlacq1628doc.pdf.
[3] D. Roegel. "A Reconstruction of Adriaan Vlacq's Tables in the Trigonometria Artificialis (1633)." (Nov 26, 2011) locomat.loria.fr/vlacq1633/vlacq1633doc.pdf.
[4] D. Roegel, "A Reconstruction of the Tables of Pitiscus' Thesaurus Mathematicus (1613)." (Dec 6, 2010) hal.inria.fr/docs/00/54/39/33/PDF/pitiscus1613doc.pdf.
[5] D. Roegel, "A Reconstruction of the Tables of Rheticus' Opus Palatinum (1596)." (Dec 6, 2010) hal.inria.fr/docs/00/54/39/32/PDF/rheticus1596doc.pdf.
[6] G. Vega, Thesaurus Logarithmorum Completus, ex Arithmetica Logarithmica, et ex Trigonometria Artificiali Adriani Vlacci, Leipzig: Weidmann, 1794.
[7] A. Vlacq, Trigonometria Artificialis, Gouda, The Netherlands: Pieter Rammazeyn, 1633.
Permanent Citation