Cellular Automata with Global Control

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
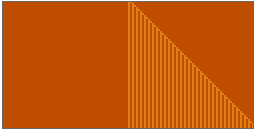
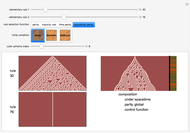
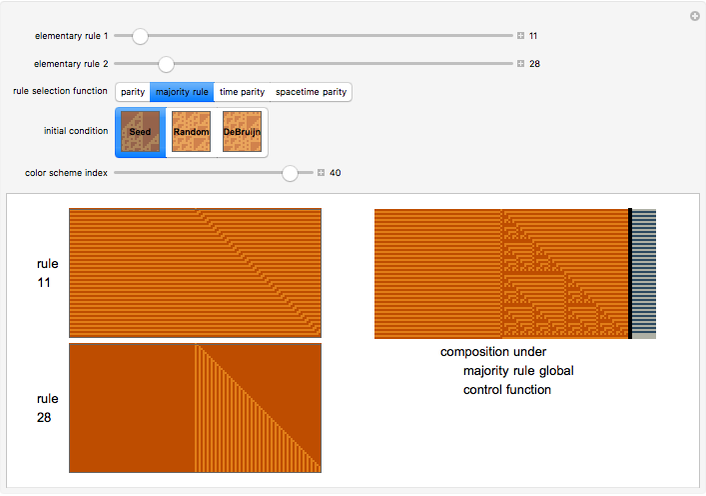
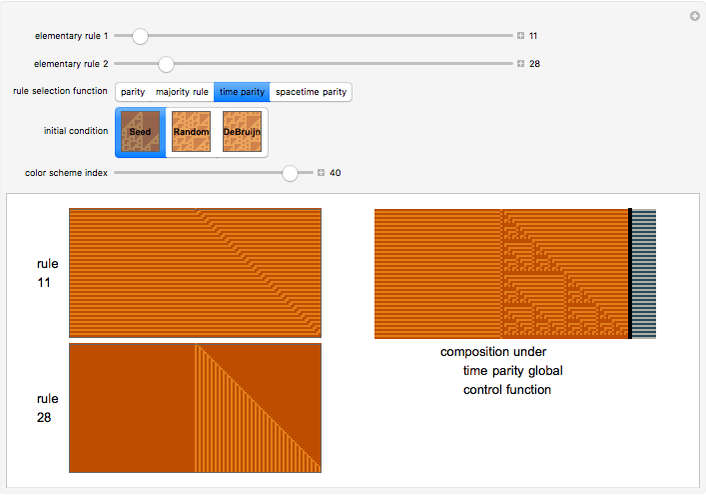
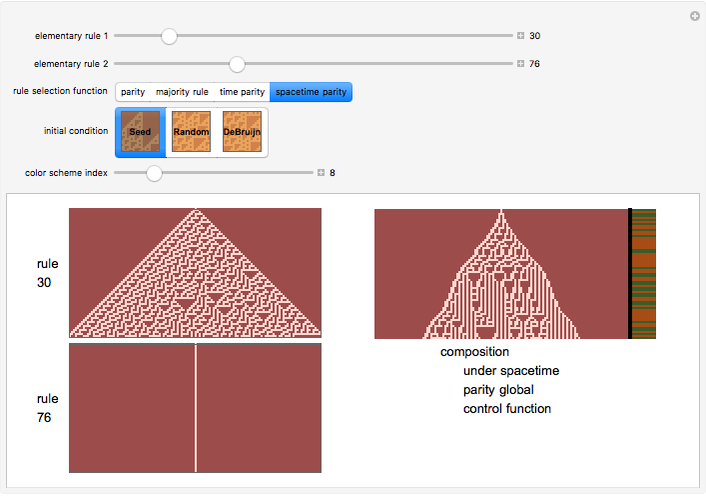
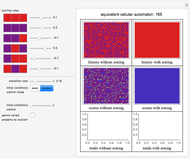
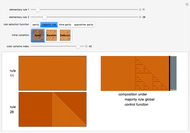
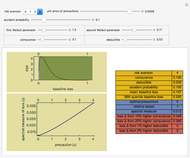
This Demonstration implements an idea of Stephen Wolfram and others of a cellular automaton that chooses the rule to apply based on the global state of the automaton. The cellular automaton is thus temporally inhomogeneous. Here, you can specify two possible elementary cellular automaton rules and four functions that choose which of the rules to apply on any given iteration. You can make two other types of choices. You can choose the initial state of the cellular automaton from amongst a seed configuration, a random configuration or a de Bruijn Sequence specification. The Demonstration outputs the results of the two elementary cellular automata and the result of the composition using the particular global control function. The elementary rule used is appended to the right of the latter plot and appears as stripes. You can also select a color scheme to optimize aesthetics.
Contributed by: Seth J. Chandler (May 2007)
After work by: Stephen Wolfram, Jason Cawley, Todd Rowland and Alastair Hewitt
Open content licensed under CC BY-NC-SA
Snapshots
Details
The "rule selection functions" may be described as follows. The parity rule uses the second rule if the parity of the cellular automaton at a given point in time is even; otherwise it chooses the first rule. The majority rule uses the second rule if the majority of the cellular automaton cells are in state 1; otherwise it uses the first rule. The remaining two functions hint at the additional capabilities of the code behind this Demonstration. The "time parity" selection function exemplifies what has been termed an interactive cellular automaton, in which the cellular automaton can be "programmed" to choose an update rule based on the iteration number; the state of the cellular automaton thus has a spatial and temporal component. Finally, the spacetime parity rule looks at the parity of the sum of (a) the parity of the cellular automaton and (b) the time parity. It thus creates the possibility of spatio-temporal interaction.
The code underlying this Demonstration should accommodate all sorts of cellular automaton rules, including those with more than 2 colors or a radius greater than 1.
The cellular automata used here all have widths fixed by their initial conditions.
Cellular automata with global control may prove quite useful in modeling interactions in which behavior depends on the behavior of neighbors and on global information produced by some sort of aggregating mechanism such as a market.
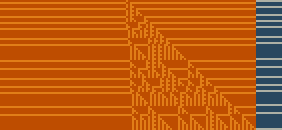
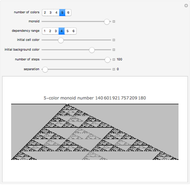
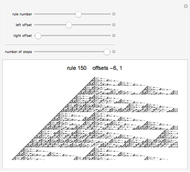
Snapshot 1: the interaction of Rule 11 and Rule 28 with majority rule function selection starting from a de Bruijn Sequence
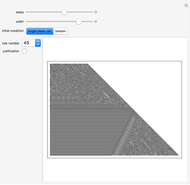
Snapshot 2: the interaction of Rule 11 and Rule 28 with time parity rule selection starting from a de Bruijn Sequence
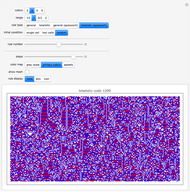
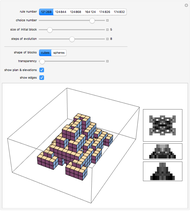
Snapshot 3: the interaction of Rule 30 and Rule 76 with spacetime parity rule selection starting from seed
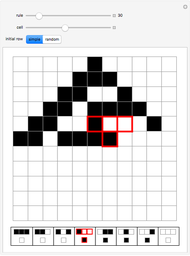
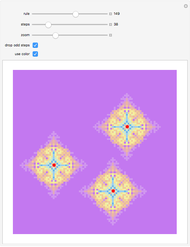
Snapshot 4: the interaction of Rule 30 and Rule 43 with time parity rule selection starting from randomness
Permanent Citation