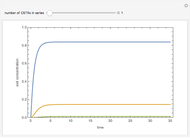
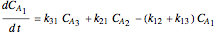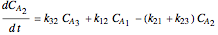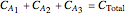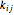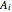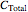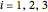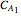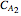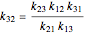Reaction Paths of Wei-Prater Complex Reaction Networks
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
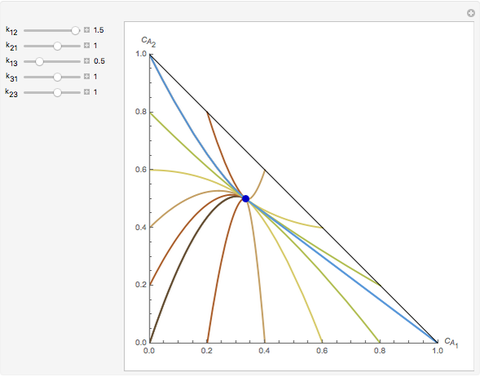
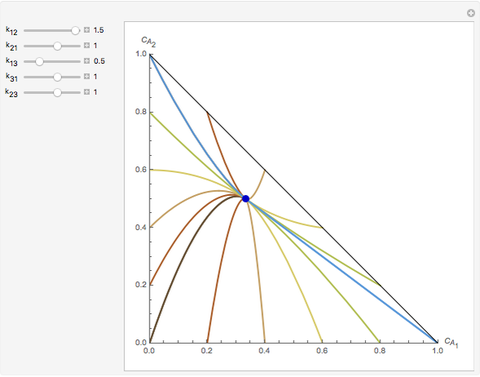
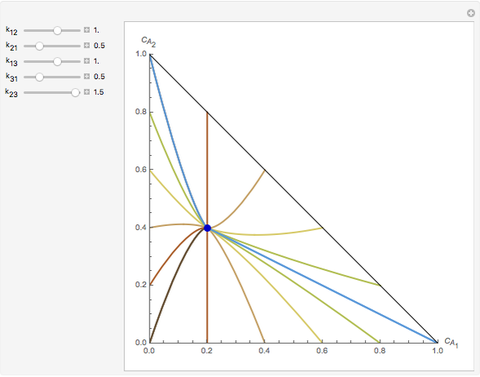
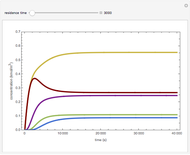
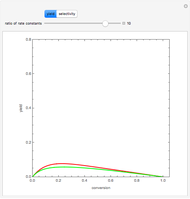
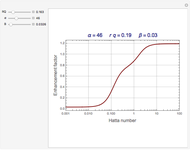
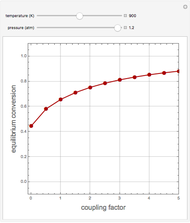
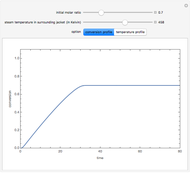
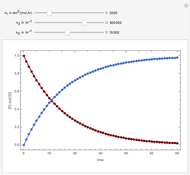
Consider the following complex reaction network, called the Wei–Prater mechanism: 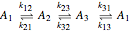 .
.
Contributed by: Housam Binous and Ahmed Bellagi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
G. F. Froment and K. B. Bischoff, Chemical Reactor Analysis and Design, 2nd ed., New York: Wiley, 1990.
Permanent Citation