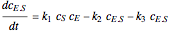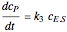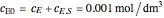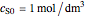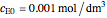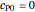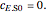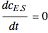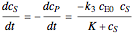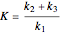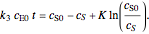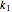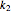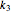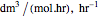Enzymatic Reaction in a Batch Reactor
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
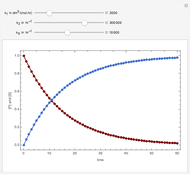
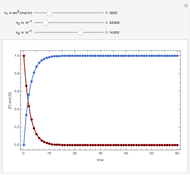
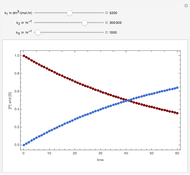
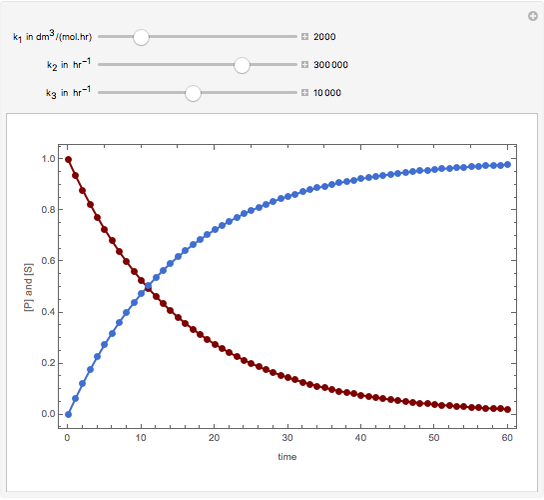
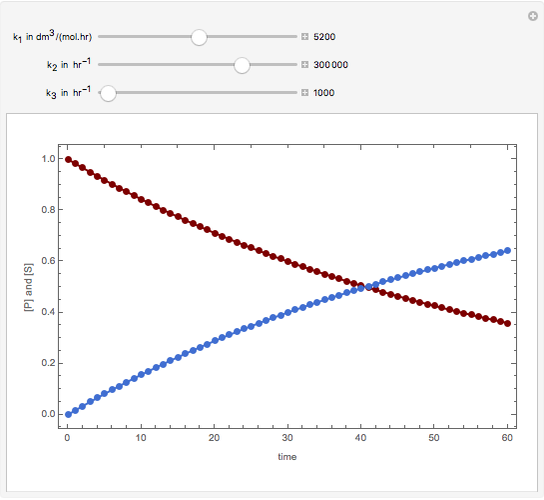
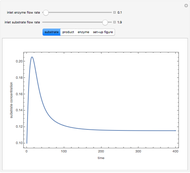
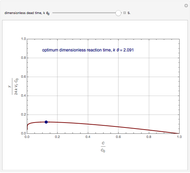
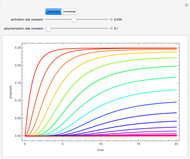
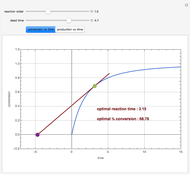
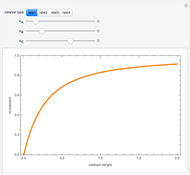
Consider the following reaction scheme:  , where
, where 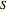 is the substrate,
is the substrate, 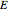 is an enzyme catalyst,
is an enzyme catalyst,  is the enzyme-substrate complex, which decomposes to give the product
is the enzyme-substrate complex, which decomposes to give the product 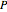 , and
, and 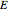 is the enzyme. This enzymatic reaction takes place in a batch reactor and the governing differential-algebraic system of equations is:
is the enzyme. This enzymatic reaction takes place in a batch reactor and the governing differential-algebraic system of equations is:
Contributed by: Housam Binous (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference: M. B. Cutlip and M. Shacham, Problem Solving in Chemical Engineering with Numerical Methods, Upper Saddle River, NJ: Prentice Hall, 1999.
Permanent Citation