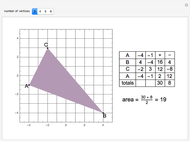
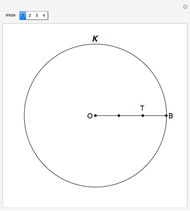
Ruffini-Horner Method for Polynomials with Rational Roots

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
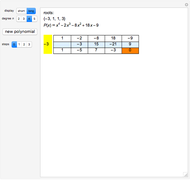
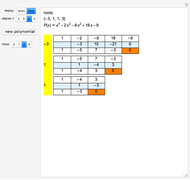
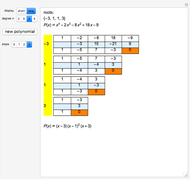
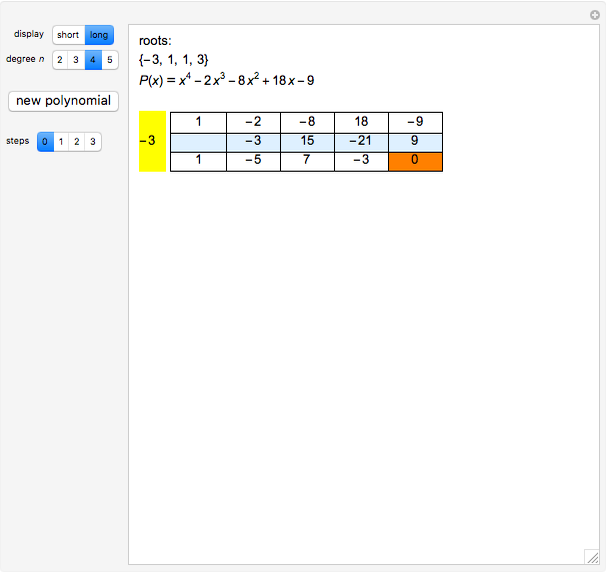
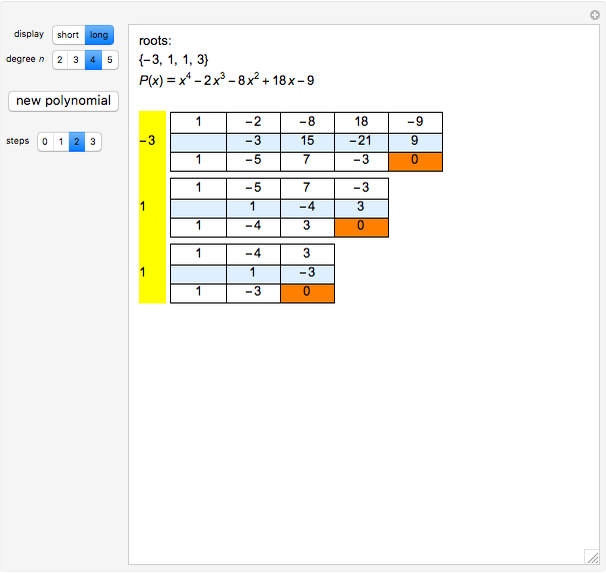
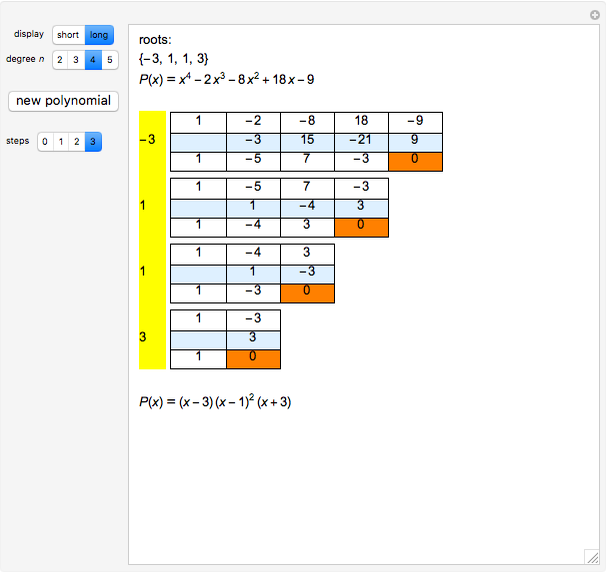
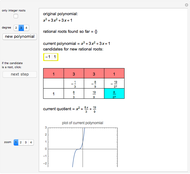
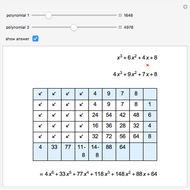
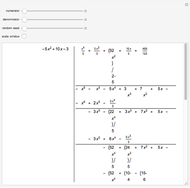
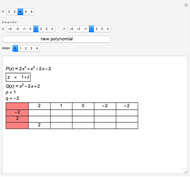
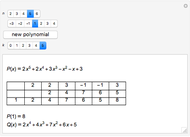
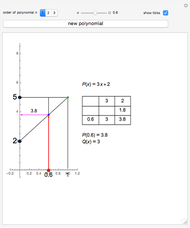
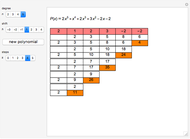
This Demonstration shows the division of a polynomial of degree  with only rational roots
with only rational roots 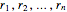 by the binomials
by the binomials 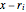 using the Ruffini–Horner method.
using the Ruffini–Horner method.
Contributed by: Izidor Hafner (February 2017)
Open content licensed under CC BY-NC-SA
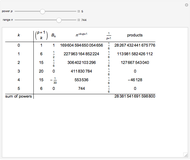
Snapshots
Details
detailSectionParagraphPermanent Citation
"Ruffini-Horner Method for Polynomials with Rational Roots"
http://demonstrations.wolfram.com/RuffiniHornerMethodForPolynomialsWithRationalRoots/
Wolfram Demonstrations Project
Published: February 24 2017