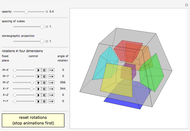
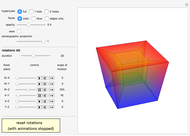
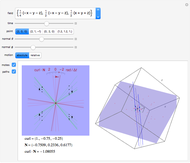
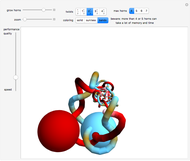
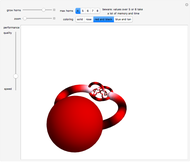
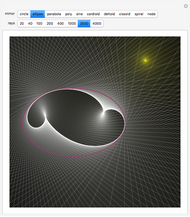
Sections of the Four-Cube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
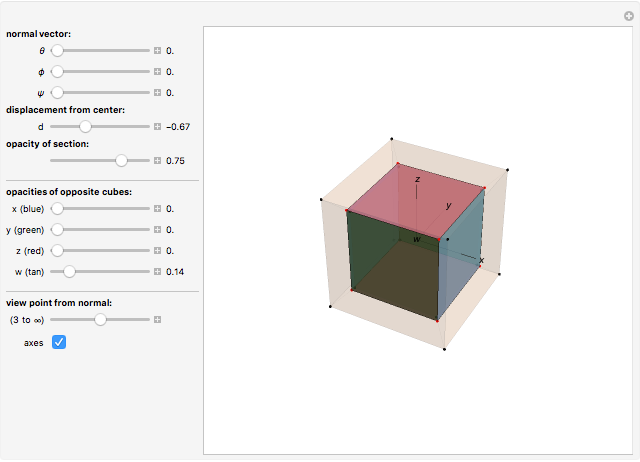
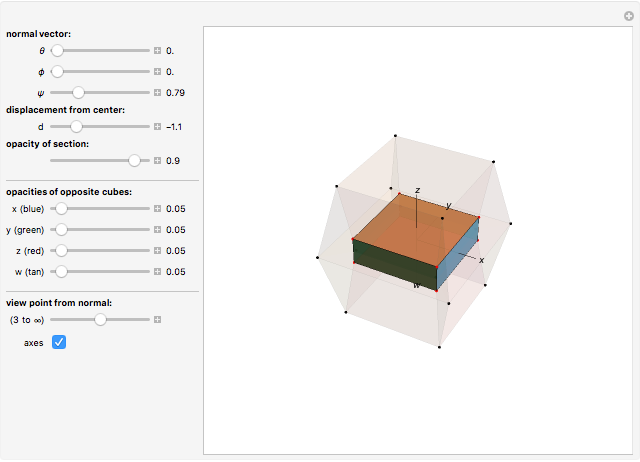
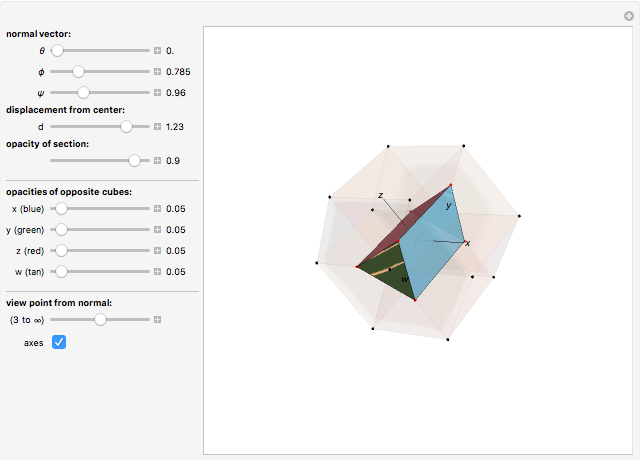
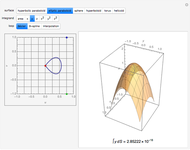
This displays the section of the 4D cube by a hyperplane orthogonal to the normal vector described by the hyperspherical coordinate angles  ,
,  , and
, and  and at a displacement
and at a displacement  from the origin along the normal. A projection of the four-cube from a view point along the normal is also shown, as well as of the
from the origin along the normal. A projection of the four-cube from a view point along the normal is also shown, as well as of the  ,
, 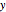 ,
,  ,
,  axes.
axes.
Contributed by: Michael Rogers (Oxford College/Emory University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The unit normal vector is controlled by the angles  ,
,  , and
, and  . The first two are just like the same angles in regular 3D spherical coordinates:
. The first two are just like the same angles in regular 3D spherical coordinates:  , with
, with 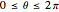 , is the angle to the positive
, is the angle to the positive  axis (or more precisely, the
axis (or more precisely, the  -
- -
- hyperplane), and
hyperplane), and  , with
, with  , is the angle to the positive
, is the angle to the positive  axis (or rather the
axis (or rather the  -
- plane). The angle
plane). The angle  , with
, with 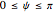 , is the angle formed by the normal and the positive
, is the angle formed by the normal and the positive  axis and is analogous to
axis and is analogous to  in that way. If
in that way. If  , then
, then  and
and  have no effect, just as when
have no effect, just as when 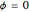 , the angle
, the angle  has no effect. When the normal is changed, it appears that the four-cube rotates. But it is not moving; it is your view point that is moving. Of course, the two kinds of motion look the same.
has no effect. When the normal is changed, it appears that the four-cube rotates. But it is not moving; it is your view point that is moving. Of course, the two kinds of motion look the same.
Animate the distance  and view the series of sections orthogonal to the normal from one end to the other. The coordinates of the vertices of the four-cube are
and view the series of sections orthogonal to the normal from one end to the other. The coordinates of the vertices of the four-cube are  , so the vertices are two units from the origin. The displacement
, so the vertices are two units from the origin. The displacement  is the displacement of the hyperplane, and thus the section consists of all points of the four-cube, the projections of whose coordinate vectors onto the normal are equal to
is the displacement of the hyperplane, and thus the section consists of all points of the four-cube, the projections of whose coordinate vectors onto the normal are equal to  times the normal.
times the normal.
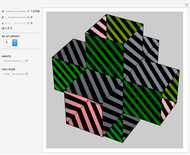
Each cell (bounding 3D cube) of the four-cube is drawn with the same color as the face of its section by the hyperplane. By playing with the opacities, you can see the relationship between the cube-cube's cells and the intersection.
The projection displayed is from a point 3 to infinity units away from the origin along the line through the origin parallel to the normal (infinity gives a parallel projection). The four-cube and section are projected onto the hyperplane through the origin and orthogonal to the normal. A 3D coordinate system for this hyperplane is attached to the normal and rotates around with it as the normal is changed. This coordinate system will "precess": as the normal moves around (you need to change at least two angles) and moves back (along a different trajectory) the section will appear to have changed position. But it has not. It is the coordinate system used to project the section onto the screen that has changed.
Some important angles: 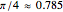 ,
, 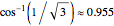 ,
,  ,
, 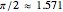 .
.
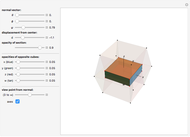
Snapshot 1: cell first (normal parallel to center of a cube-cell): cube
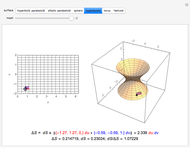
Snapshot 2: face first (normal parallel to center of a 2D face): rectangular box with a square face
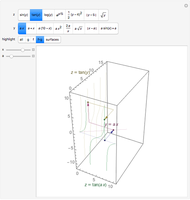
Snapshot 3: edge first (normal parallel to midpoint of edge): equilateral-triangular prism
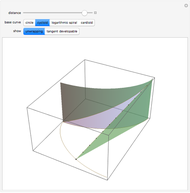
Snapshot 4: vertex first (normal parallel to midpoint of vertex): regular tetrahedron
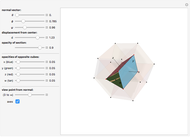
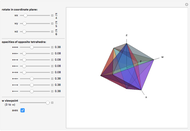
Snapshot 5: hexagonal prism
Snapshot 6: regular octahedron
Permanent Citation