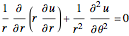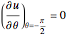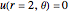Steady-State Heat Conduction in an Annulus
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
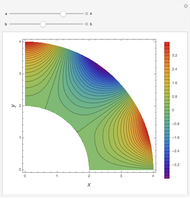
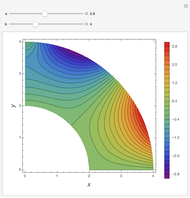
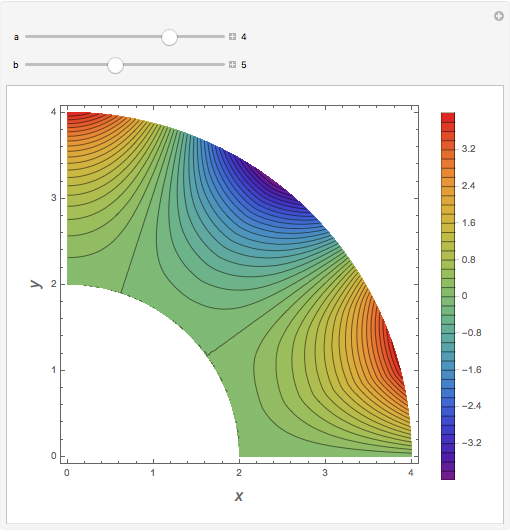
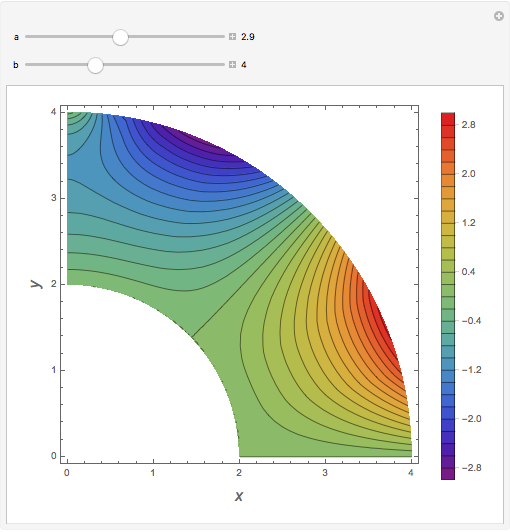
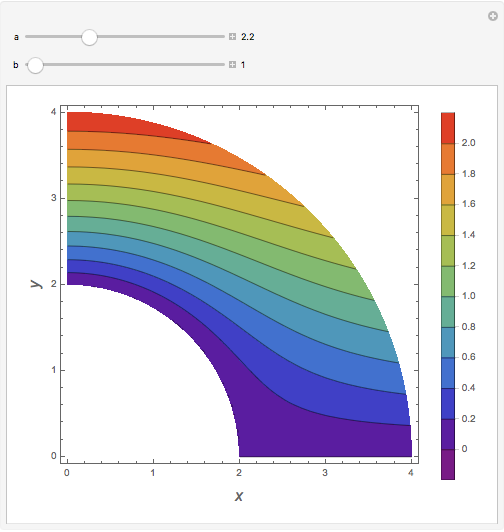
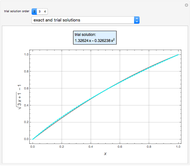
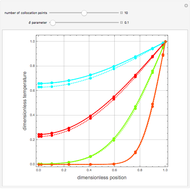
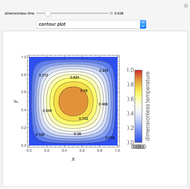
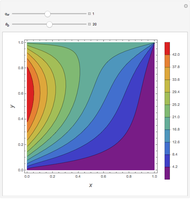
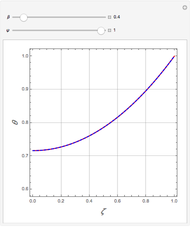
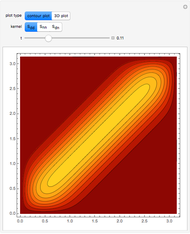
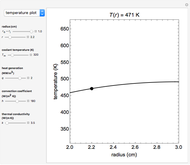
Consider steady-state heat conduction in an annulus with periodic boundary condition.
[more]
Contributed by: Housam Binous and Ahmed Bellagi (August 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation