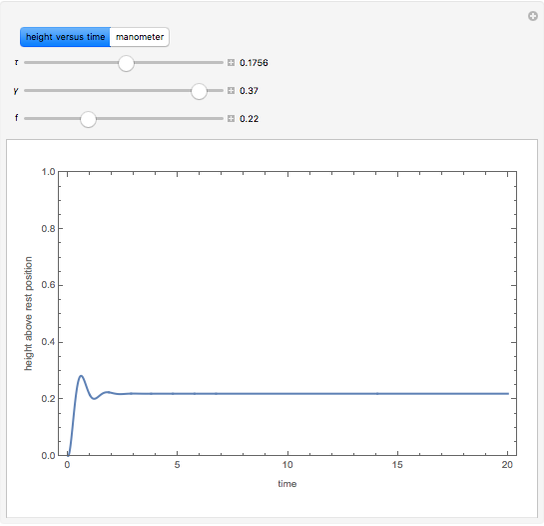
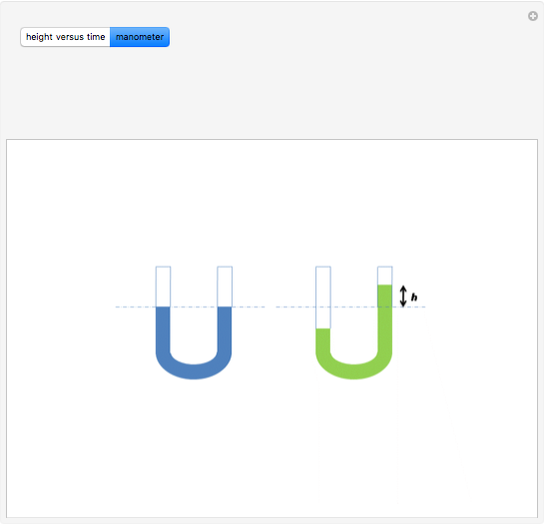
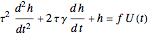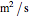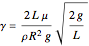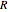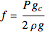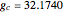Step Response of a Manometer

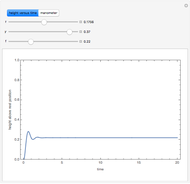
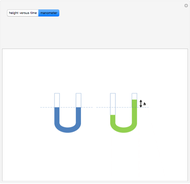
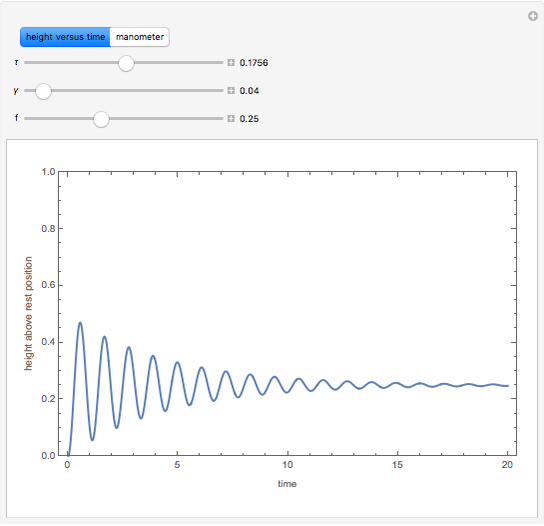
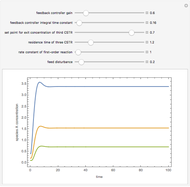
A manometer is an instrument for measuring pressure. It consists of a U-shaped tube filled with liquid (usually mercury because of its high density). The difference, 2 , between the heights of the liquid is a function of the pressure difference between the two sides.

The step response of a manometer obeys the following equation:

,

where is the unit-step function, is the height above the rest position, ( is a time constant), is the total height of the manometer, and is the acceleration due to gravity. Also, is a damping coefficient, where is the viscosity, is the density, is the radius of the manometer, and is proportional to the applied gas pressure, where is a unit conversion factor.

This Demonstration shows the height above the rest position versus time. The observed behavior is typical of a second-order process. The overshoot observed in the step response of the manometer, for small values of the damping coefficient, makes it easy for manometers to overflow.