Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Estimating and Diagnostic Checking in Censored Normal Random Samples

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

A random sample of size is simulated from either a normal or scaled distribution with mean 100 and standard deviation 15. It is then left-censored corresponding to a detection level , where is the censor rate and is the inverse normal cumulative distribution function. The plot shows the data quantiles plotted against the corresponding quantiles in a normal distribution with mean and standard deviation , where and are estimates that are initially set to 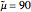and . We imagine a robust fitting line that passes through the bulk of the points. Then adjusting shifts the location of this line while shifts its slope. By adjusting and dynamically using the controls, we can find parameter values for which the hypothetical line lies on the 45° line. In other words, the bulk of the data will lie on the 45° line.

[more]

If there are outliers in the data, as is frequently the case with data generated from the scaled distribution, this dynamic graphical method provides a more robust estimation method than Gaussian maximum likelihood and so may produce better estimates of the true parameters and . You can investigate the effect of sample size, censoring, and randomness by varying , , and , respectively. The normal distribution is used in the plot shown in the thumbnail.

This dynamic approach provides not only a robust estimation method but also a diagnostic plot to check the assumption of normality when Gaussian maximum likelihood estimates are used. The approach outlined here can be extended for robust estimation with other distributions, including the log-normal and gamma.

[less]

Contributed by: Nagham Muslim Mohammad and Ian McLeod (August 2013)
(Department of Statistical and Actuarial Sciences, Western University)
Open content licensed under CC BY-NC-SA

Snapshots

Details

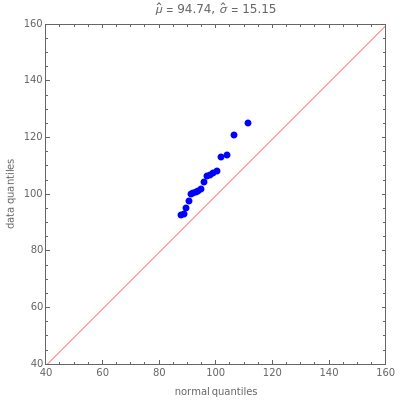
Snapshot 1: by using the maximum likelihood estimates (i.e., setting, and ), we can use this plot as a model diagnostic to check the adequacy of the normality assumption; in this case, we conclude the model is adequate

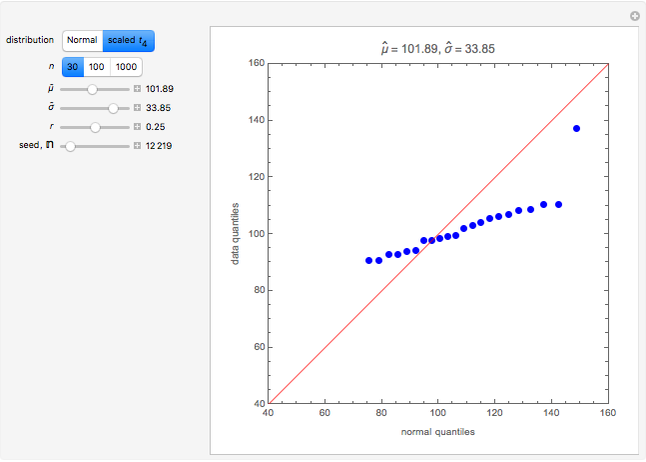
Snapshot 2: the data was generated from the scaled distribution and is not well fit using the Gaussian MLE

Snapshot 3: a better fit and better estimates of the true parameter values and to the data shown in snapshot 2 are obtained by using the dynamic graph

Gaussian maximum likelihood estimation is often used to estimate the mean and standard deviation in normal random samples [1]. As suggested in [2], the EM algorithm provides an effective algorithm for implementing Gaussian maximum likelihood estimation with censored samples, and this method is used in this Demonstration.

References

[1] M. S. Wolynetz, "Algorithm AS 138: Maximum Likelihood Estimation from Confined and Censored Normal Data," Journal of the Royal Statistical Society. Series C (Applied Statistics), 28(2), 1979 pp. 185–195.

[2] C. R. Robert and G. Casella, Monte Carlo Statistical Methods, New York: Springer, 2004.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send