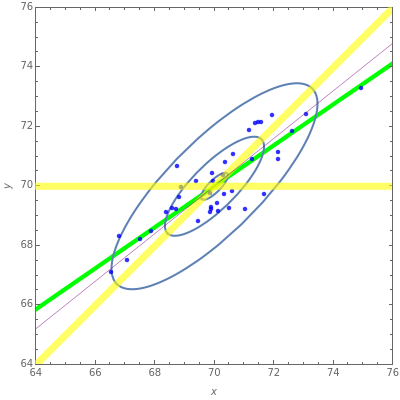
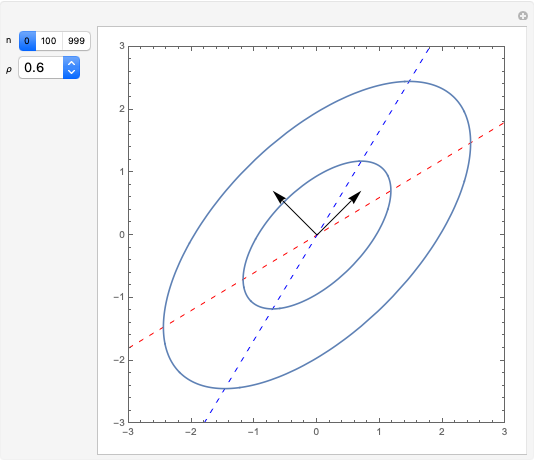
Regression owes its name to the phenomenon known as regression toward the mean that arises when a genetically determined characteristic, such as height, is correlated between parent and offspring. This results in a regression line, offspring height on parent height, that is characterized by a tall parent's offspring also being tall but less so, on average, than the parent and, similarly, a short parent's offspring also being short but not as short as the parent. Assuming that the univariate distributions of the parent and offspring are the same, this implies that the expected regression line will be less than the line for large values of the characteristic, and conversely for small values. The two yellow lines correspond to or equivalently , where is the correlation and , the mean, or equivalently . 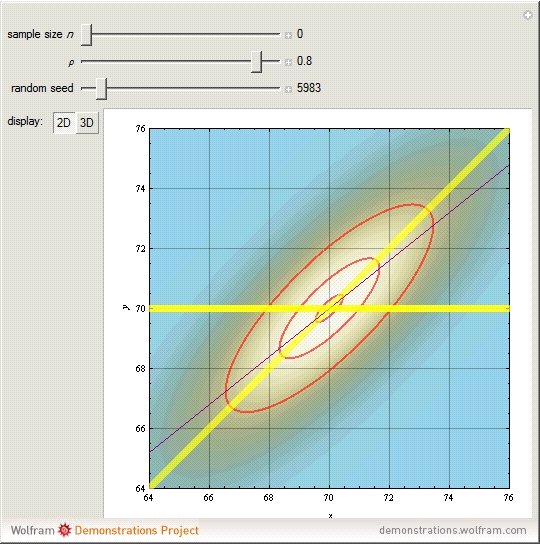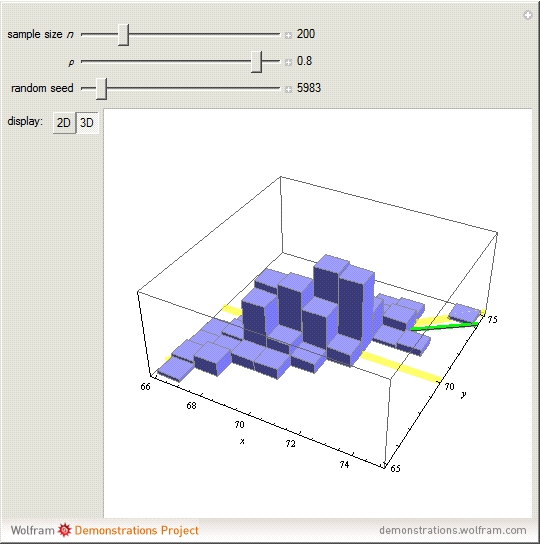When 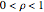, the thin purple line, the expected regression line, is always between the two yellow lines demonstrating regression toward the mean. The red ellipses show the ellipsoids of concentration corresponding to 95%, 50%, and 5% probability in the bivariate normal distribution. The blue points are data simulated from the regression, and the green line shows the fitted regression line. In some cases, especially when the sample size is small, regression toward the mean may not hold for the fitted regression line. A 3D visualization is also provided. When , only the purple expected regression line 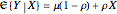, where 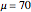, and the concentration ellipsoids for the bivariate distribution are shown on a background generated by the DensityPlot[]. See the Details section for further discussion.