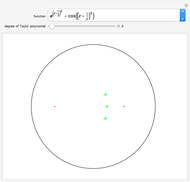
Counting the Number of Roots of Transcendental Functions in Bounded Regions Using Winding Numbers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
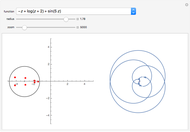
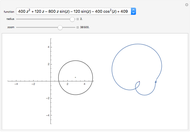
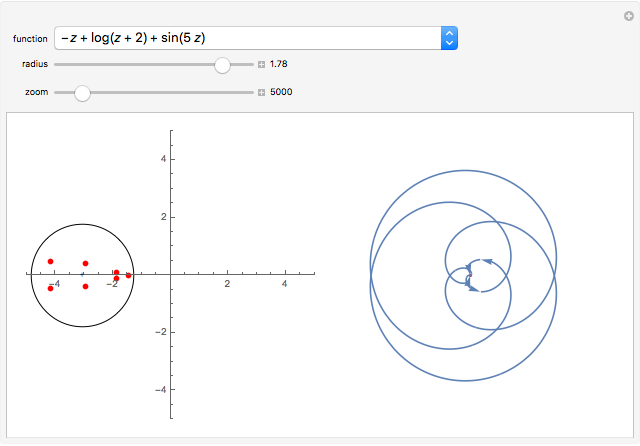
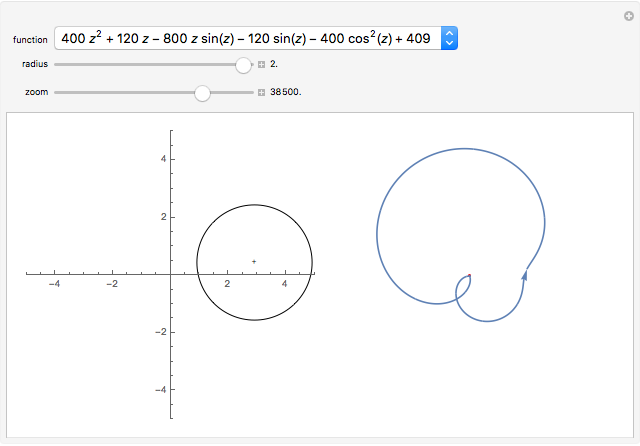
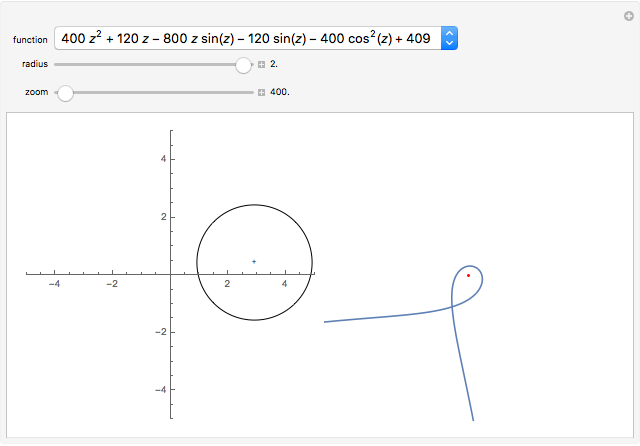
For a given analytic function 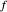 chosen from the popup menu, a circle radius
chosen from the popup menu, a circle radius  chosen using a slider, and a circle center denoted by "+" (which can be dragged), the graphic on the left shows the roots of
chosen using a slider, and a circle center denoted by "+" (which can be dragged), the graphic on the left shows the roots of 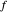 inside the disk of radius
inside the disk of radius  . The graphic on the right shows the image of the circle under the map
. The graphic on the right shows the image of the circle under the map 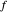 and the origin of the coordinate system. According to the argument principle, the number of roots of
and the origin of the coordinate system. According to the argument principle, the number of roots of  (counted with multiplicities) inside the disk is equal to the winding number of the image of the circle around the origin.
(counted with multiplicities) inside the disk is equal to the winding number of the image of the circle around the origin.
Contributed by: Andrzej Kozlowski (August 2011)
Open content licensed under CC BY-NC-SA
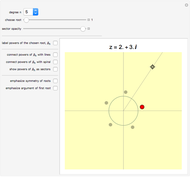
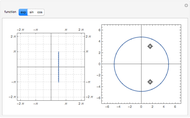
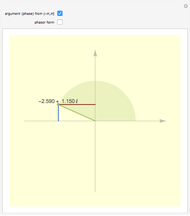
Snapshots
Details
The argument principle is usually stated in integral form: for a function 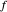 that is continuous on a simple curve
that is continuous on a simple curve 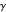 and analytic inside
and analytic inside 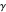 , the number of zeros of
, the number of zeros of 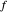 inside
inside 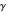 is given by the path integral
is given by the path integral 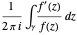 . By making the substitution
. By making the substitution  , we see that the number of roots inside
, we see that the number of roots inside 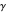 is
is  , where
, where 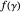 denotes the image of the curve
denotes the image of the curve 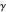 under
under 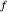 . This is the winding number of the curve
. This is the winding number of the curve 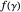 with respect to the origin. This fact can be used to find the number of roots of analytic functions in bounded regions, a key step in finding the roots themselves [1].
with respect to the origin. This fact can be used to find the number of roots of analytic functions in bounded regions, a key step in finding the roots themselves [1].
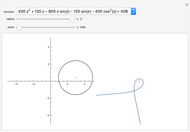
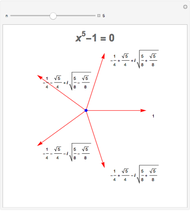
Recall from [1] that the winding number of an oriented closed curve around the origin can be computed as follows. If the origin lies on the outside of the closed curve, the winding number is 0. Otherwise, one draws a line from the origin to any point lying outside the curve and counts the number of intersection points (including multiplicities). Intersections where the curve is moving leftward are counted with a plus sign and the ones where the curve is moving rightward with a minus sign. By computing the winding number visually using the picture on the right-hand side one can check that it agrees with the number of roots enclosed by the curve on the left. Sometimes to compute the winding number visually one needs to zoom in and out. This is illustrated in snapshots 2 and 3. In this case there are no roots enclosed by the curve, so the winding number is 0. Looking only at snapshot 2 we could think that the winding number is one, however zooming in on the origin in snapshot 3 shows that it is indeed 0.
References
[1] P. Kravanja and M. Barel, Computing the Zeros of Analytic Functions, New York: Springer, 2000.
[2] T. Needham, Visual Complex Analysis, Oxford: Oxford University Press, 1998.
Permanent Citation