The Swallowtail Singularity

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
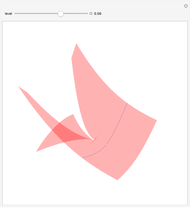
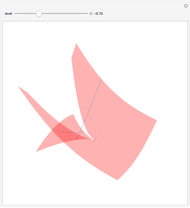
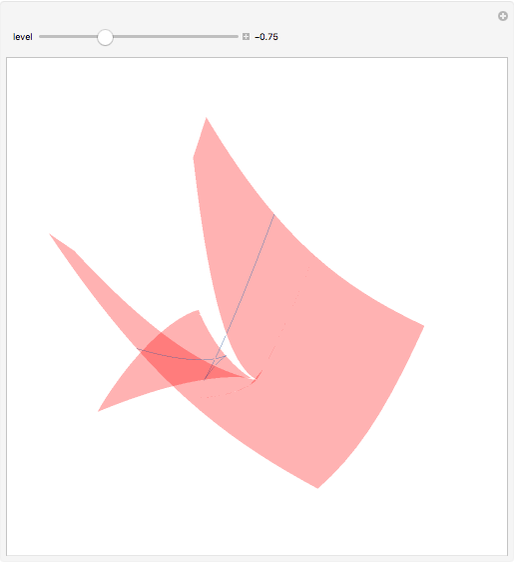
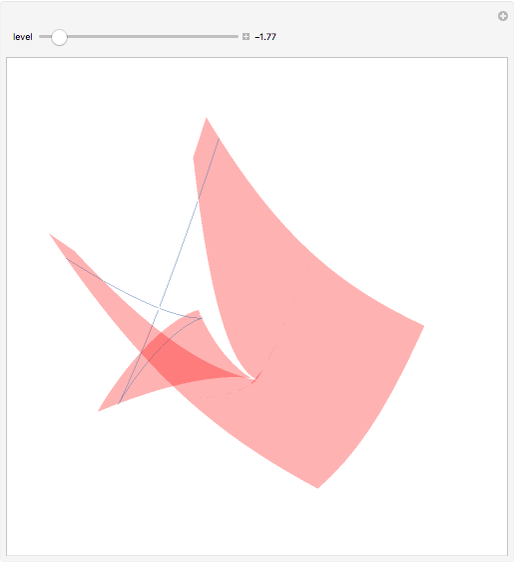
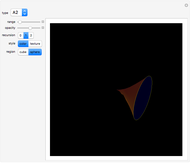
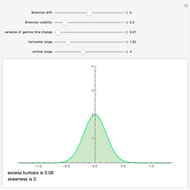
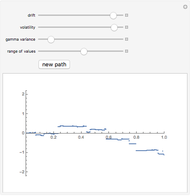
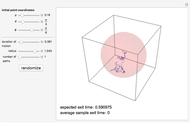
This Demonstration shows one of the most frequently occurring objects in singularity theory: the swallowtail singularity. It is realized here as the subspace of 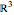 consisting of all points
consisting of all points 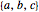 such that
such that  has multiple real roots. In addition, a section of the singularity surface by a plane
has multiple real roots. In addition, a section of the singularity surface by a plane  is shown as a blue line. Such a section is a plane curve. As the level
is shown as a blue line. Such a section is a plane curve. As the level  varies, the curve undergoes a metamorphosis (or a perestroika), which is exactly the same as that of a wave front on a plane.
varies, the curve undergoes a metamorphosis (or a perestroika), which is exactly the same as that of a wave front on a plane.
Contributed by: Andrzej Kozlowski (September 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The swallowtail surface has many equivalent definitions. Among them: the swallowtail is the codimension-three stratum of the caustic (and the Maxwell set) of the space of all smooth mappings from the real line to itself. It is also a singularity that appears during the propagation of a generic smooth wave front in three-dimensional space. The swallowtail singularity remains stable under small perturbations. Its sections by generic horizontal planes are plane curves describing wave fronts on a plane, and so on.
The swallowtail surface was the subject of the last painting of Salvadore Dali, entitled The Swallow's Tail,inspired by René Thom's lectures on catastrophe theory.
Reference
[1] V. I. Arnold, The Theory of Singularities and Its Applications, Cambridge, UK: Cambridge University Press, 1993.
Permanent Citation
"The Swallowtail Singularity"
http://demonstrations.wolfram.com/TheSwallowtailSingularity/
Wolfram Demonstrations Project
Published: September 18 2012