Standard American and European Options

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
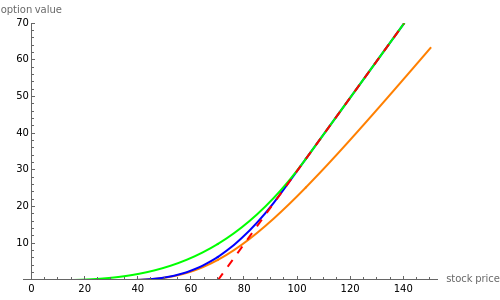
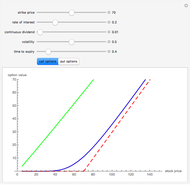
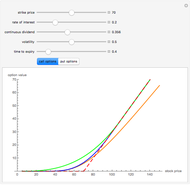
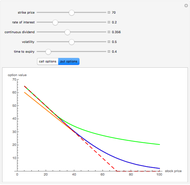
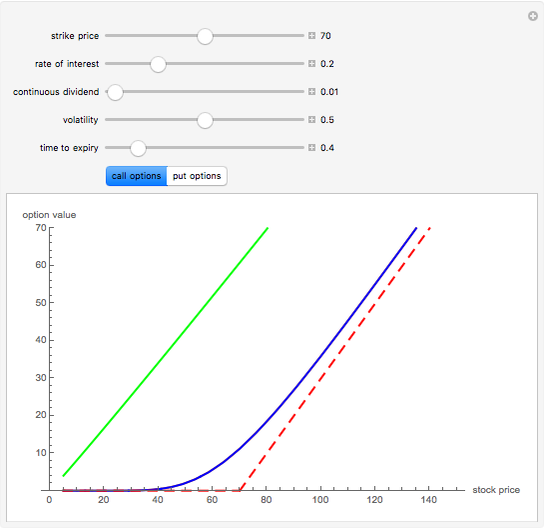
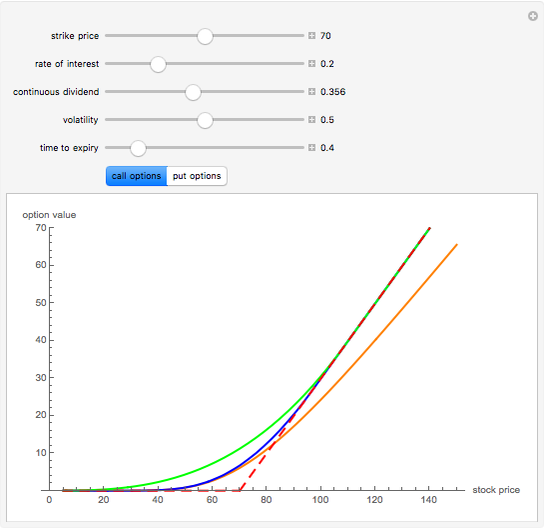
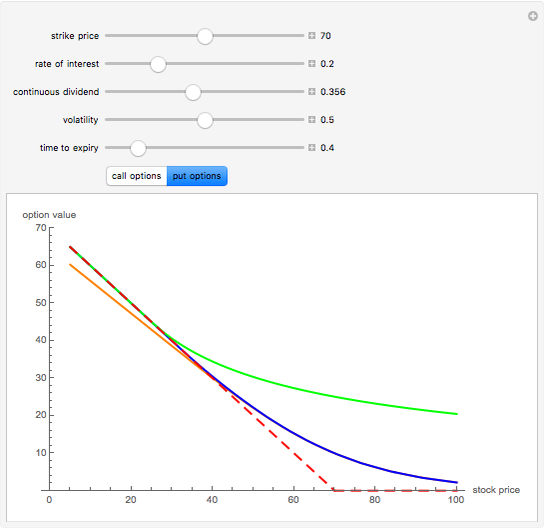
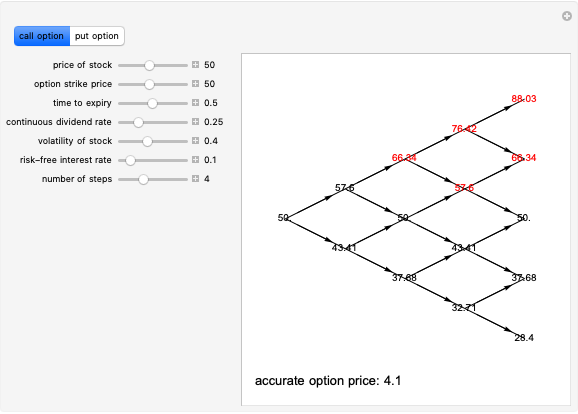
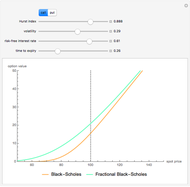
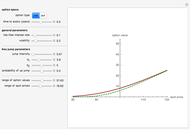
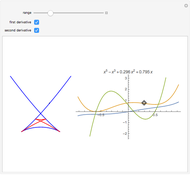
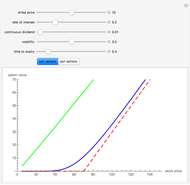
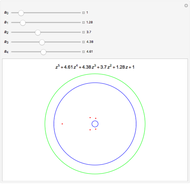
This Demonstration explores graphically the relationship between standard American and European options on securities. The graph shows one straight line and three curves. The dashed red straight line (together with a part of the  axis) represents the payoff function of a European option (call or put, depending on the user's choice). The orange curve represents the values of a standard European option, the blue curve a standard American option, and the green curve the perpetual (time-independent) option. You can hover over a curve to see what it represents.
axis) represents the payoff function of a European option (call or put, depending on the user's choice). The orange curve represents the values of a standard European option, the blue curve a standard American option, and the green curve the perpetual (time-independent) option. You can hover over a curve to see what it represents.
Contributed by: Andrzej Kozlowski (July 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The value of a standard European option as well as a "perpetual" option (an option that can be exercised at any time and never expires) can be computed using a explicit "closed formula" (the so-called Black–Scholes formula). However, no such formula is known for the value of an American option, so a numerical procedure has to be used. Here we use the binomial tree method (c.f. the American Call and Put Option Demonstration). There are a number of relationships between values of these options that can be observed by studying this Demonstration. Since an American option has more "optionality" than a corresponding European one, its value is always at least as large. On the other hand, the value of an American option is obviously never larger than that of a perpetual option (with the same values of the relevant parameters). Both the American and the perpetual options never lie below the payoff line (but a part of a European option curve may lie below the payoff line). A point where an American or perpetual option curve touches the payoff line (the point lies above the payoff line on one side and coincides with it on the other) represents the value of the stock for which early exercise is optimal. It is known that for a zero dividend (and non-negative interest rate) early exercise of an American (or perpetual) call option is never optimal, hence in this case the American option curve coincides with the corresponding European one.
Perpetual options do not correspond to any financial instrument that is actually sold on any stock exchange. However, American call options play an important role in stochastic investment theory; see A. K. Dixit and R. Pindick, Investment Under Uncertainty, Princeton, NJ: Princeton University Press, 1994.
Permanent Citation