The Vieta Mapping for the Coxeter Group 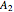

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
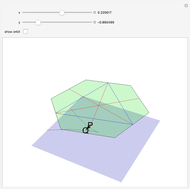
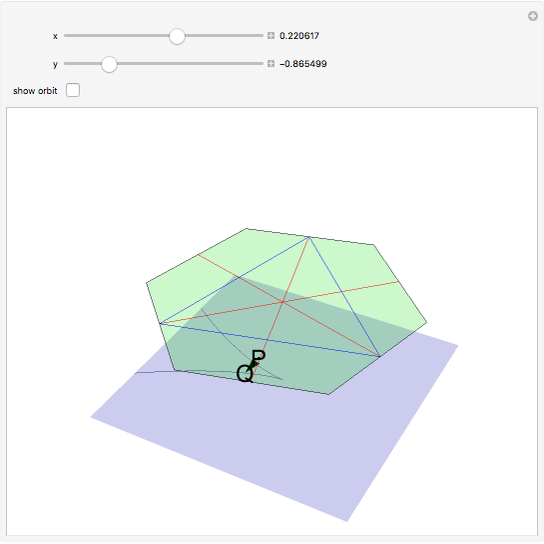
This Demonstration shows the real part of the Vieta mapping, which is important in singularity theory. The domain is the plane 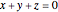 containing the green hexagon; it has been rotated around the origin to make it horizontal for the purpose of the Demonstration. A point
containing the green hexagon; it has been rotated around the origin to make it horizontal for the purpose of the Demonstration. A point  in the plane determines a polynomial
in the plane determines a polynomial 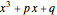 with roots
with roots  ,
, 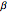 ,
,  . The image
. The image 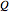 of
of 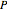 (the tip of the arrow from
(the tip of the arrow from 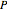 ) has coordinates
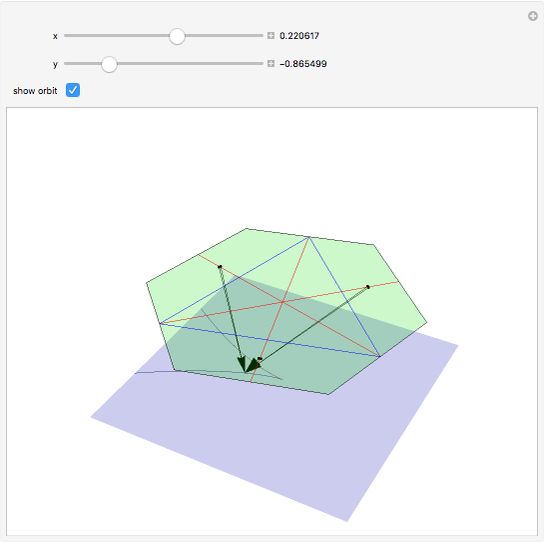
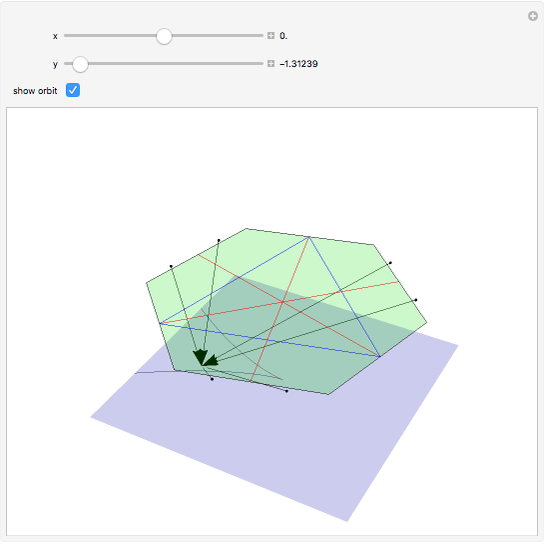
) has coordinates 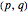 . When the "show orbit" checkbox is checked, the orbit of the point
. When the "show orbit" checkbox is checked, the orbit of the point 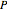 under the action of the Coxeter group
under the action of the Coxeter group 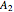 generated by reflections in the red lines (or symmetries of the blue equilateral triangle) is shown together with the image of all the points in the orbit (the set of all the distinct images of the point under transformations by elements of the group
generated by reflections in the red lines (or symmetries of the blue equilateral triangle) is shown together with the image of all the points in the orbit (the set of all the distinct images of the point under transformations by elements of the group 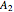 ).
).
Contributed by: Andrzej Kozlowski (October 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Coxeter group 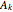 acts on the plane
acts on the plane  by permuting the coordinates. The space of its complex orbits can be identified with the space of polynomials
by permuting the coordinates. The space of its complex orbits can be identified with the space of polynomials 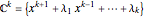 , which is a smooth manifold. The Vieta map
, which is a smooth manifold. The Vieta map 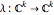 ,
, 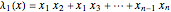 , …,
, …, 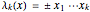 sends the space where the reflection group
sends the space where the reflection group 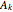 acts to the space of its orbits. The critical set of the Vieta map is the union of its mirrors. The variety of irregular orbits of a reflection group (orbits with less than the maximal number of points) are called its discriminant. The discriminant of the group
acts to the space of its orbits. The critical set of the Vieta map is the union of its mirrors. The variety of irregular orbits of a reflection group (orbits with less than the maximal number of points) are called its discriminant. The discriminant of the group 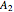 shown in this Demonstration is the semicubical parabola in the target plane of the Vieta map. The image of the real plane under the Vieta mapping is the interior of the semicubical parabola.
shown in this Demonstration is the semicubical parabola in the target plane of the Vieta map. The image of the real plane under the Vieta mapping is the interior of the semicubical parabola.
Reference
[1] V. I. Arnold, The Theory of Singularities and Its Applications, New York: Lezioni Fermiane, 1993.
Permanent Citation