Time-Dependent Scattering in the Causal Interpretation of Quantum Theory

This Demonstration shows an analytic time-dependent Gaussian wave packet with initial width and group velocity u in the (, ) space, which is reflected by a potential with an infinite wall at . The wavefunction is given by: , where 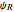and are solutions of the free Schrödinger equation 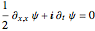with 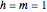. 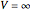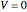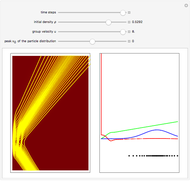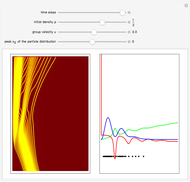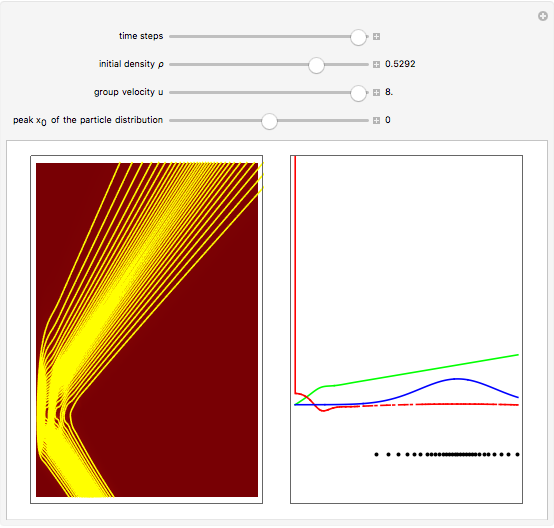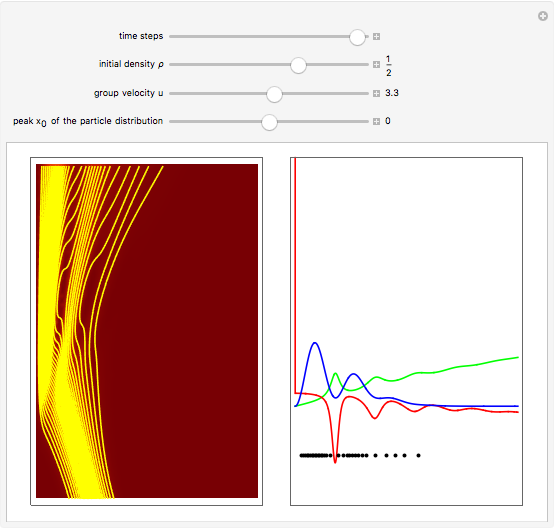The superposition of the two wavefunctions satisfies the boundary condition , which can be interpreted as the behavior of a quantum particle in a potential with for and for 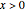. This method is similar to image methods in electrostatics. The motion of the particles is obtained by integrating the gradient of the phase function from the eikonal form of the wavefunction. To show how the evolution of the particle depends on its initial position, the starting points are arranged in a Gaussian distribution around the peak inside the wave, not related to the actual Gaussian distribution of the wavefunction. Trajectories never cross and no particles ever reach the wall. They are brought to rest, turned around, and follow the maximum of the squared wavefunction (pattern of fringes). The particles never tunnel through the wall, with those on the rear side of the packet "bouncing" back far from the wall. This is a nonclassical feature of the Bohm model. In the causal interpretation, the motion of the particles is guided by the sum of the potential and the quantum potential; the trajectories can never be measured directly.

The left side of the graphic shows the squared wavefunction and the complete trajectories. The right side shows the particles' position, the squared wavefunction (blue), the quantum potential (red) and the velocity (green). The quantum potential and the velocity are scaled to fit.