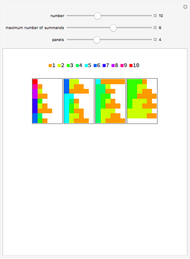
The Number of Partitions into Odd Parts Equals the Number of Partitions into Distinct Parts

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In 1748 Euler proved that for any  , the number of partitions of
, the number of partitions of  into odd parts is the same as the number of partitions of
into odd parts is the same as the number of partitions of  into distinct parts. This Demonstration shows how to go from either type to the other and back.
into distinct parts. This Demonstration shows how to go from either type to the other and back.
Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
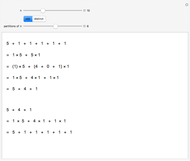
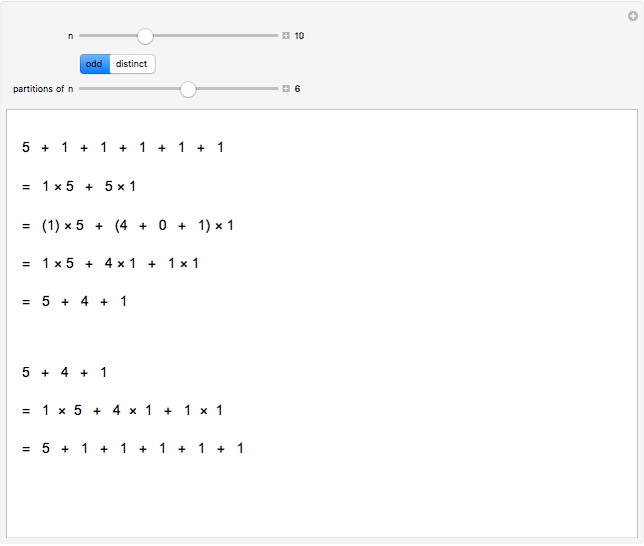
To go from an odd partition 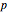 to a distinct partition, first collect the parts,
to a distinct partition, first collect the parts,  , so that
, so that  are distinct odd numbers. Write each corresponding
are distinct odd numbers. Write each corresponding 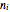 as a binary number,
as a binary number, 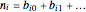 , where
, where 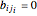 or
or 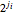 ,
, 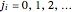 . Multiplying out all terms gives a sum of distinct parts,
. Multiplying out all terms gives a sum of distinct parts, 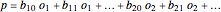 , because the
, because the 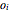 are distinct and the
are distinct and the 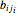 are distinct for a given
are distinct for a given 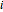 .
.
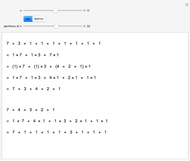
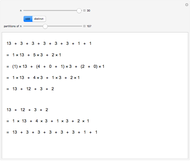
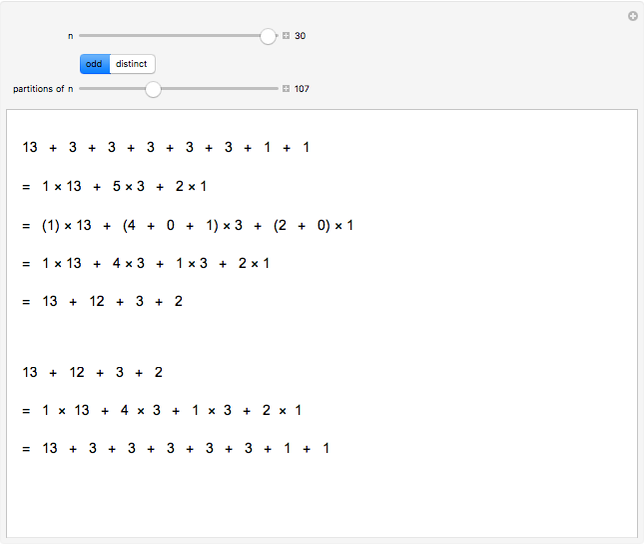
Going the other way, from a distinct partition  , let
, let 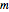 be a typical part. Let
be a typical part. Let  be the highest power of 2 dividing
be the highest power of 2 dividing 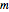 . Factor
. Factor 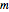 as
as 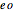 and write
and write 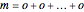 , where there are
, where there are  summands
summands  . This is a sum of odd parts. Do this for each distinct part to partition
. This is a sum of odd parts. Do this for each distinct part to partition  into odd parts.
into odd parts.
These two constructions are inverses of each other, so the set of odd partitions and the set of even partitions have the same size.
Permanent Citation