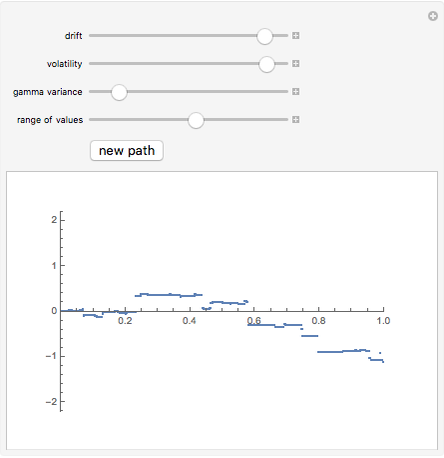
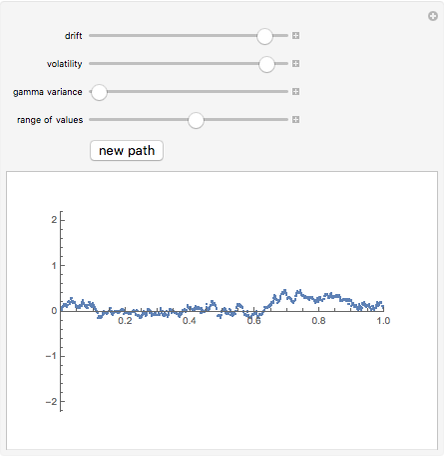
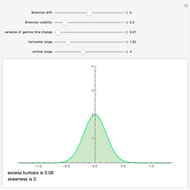
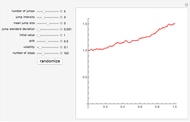
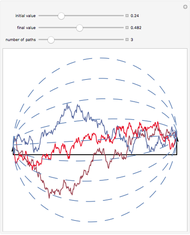
This Demonstration shows the path of a variance gamma process, a pure jump process of finite variation, but with infinitely many jumps. This process has been used in option pricing in place of Brownian motion, generally producing answers that agree better with empirical evidence. The process is constructed by means of "Brownian subordination", that is, by evaluating Brownian motion with drift at random times given by a gamma process. There are three basic controls: the volatility and drift of the Brownian motion and the variance of the gamma process. These parameters allow you to control the skewness and kurtosis of the return distribution in addition to mean and variance, as is the case with models based on Brownian motion.
The last control, "range of values", makes it possible to zoom into the process to see the jumps when they are too small to be visible in the default view or when parts of the trajectory lie outside the displayed area.
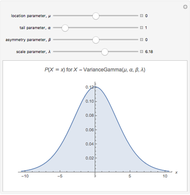
The variance gamma stochastic process is a three-parameter generalization of the Brownian motion process. It is an example of the finite variation Lévy process. It has infinitely many jumps in any time interval, but only finitely many jumps larger than any given size. Like all finite variation processes, it can be written as the difference of two increasing processes, in this case gamma processes.
The variance gamma process was introduced into option pricing by Madan and Seneta [1] and generalized by Madan, Carr, and Chang [2]. Explicit formulas for European style options can be given, generalizing the Black–Scholes formulas. The model has been shown to perform better than the Black–Scholes model under the "historical approach" [3].
[1] D. B. Madan and E. Seneta, "The Variance Gamma Process (V.G.) Model for Share Market Returns," Journal of Business63(4) pp. 511-524.
[2] D. B. Madan, P. P. Carr, and E. C. Chang, "The Variance Gamma Process and Option Pricing," European Finance Review2(1), 1998 pp. 79-105.
[3] K. Lam, E. Chang, and M. C. Lee, "An Empirical Test of the Variance Gamma Option Pricing Model," Pacific Basin Finance Journal10(3), 2002 pp. 267-285.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Browse all topics
